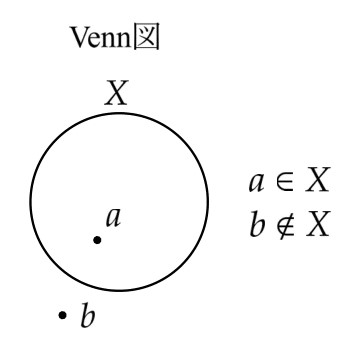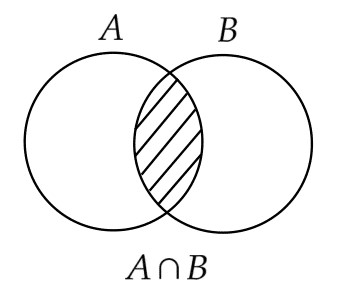集合の基本的な用語、集合の演算
集合の基本的な用語、集合の演算
集合
- 集合とは（有限個とは限らない）「ものの集まり」である
- 「あるもの」 $x$ が集合 $X$ に属することを「 $x$ は $X$ の元（げん）である」あるいは「 $x$ は $X$ の要素である」といい、$x \in X$と書く。元でないときは $x \notin X$と書く。
- 集合の元が含まれているかどうかを考えるとき、あるいは集合がいくつか与えられたとき、その様子を視覚的に見るのに$\textrm{Venn}$図（ベン図）が有用である。
- 集合 $X$ を「幾何学的な空間」として考えているとき $x \in X$ を元ではなく点ということがある。
- 集合 $X$ に対して、要素の数が有限個のとき $X$ は有限集合であるといい、そうでないとき $X$ は無限集合であるという。
- 集合の要請として、与えられた「もの」 $x$ が考えている集合 $X$ に属するかどうかは決まっているものとする。（我々の研究不足により分からなかったとしても$ x \in X$ か $ x \notin X$ のどちらであるかは決定されているものとする）
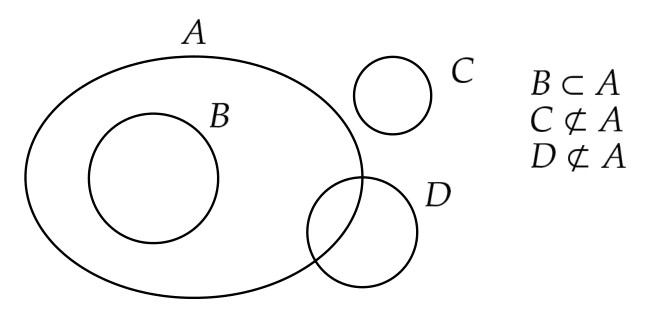
- $2$ つの集合 $A,B$ に対して、$B$ は $A$ の部分集合（ $A$ は $B$ を含むとか包含する ともいう ）であるとは、「 $B$から任意に元 $x$ をとってきたとき、その $x$ が $A$ の元でもあること」をいう。つまり、「 $ x \in B \Rightarrow x \in A $ が真である」ことである。このとき $B \subset A$ あるいは $ A \supset B$と書き、このような関係を包含関係という。$B \subset A$ でないとき $B \not\subset A$ と書く。
- $A \subset B $ かつ $ B \subset A$ のとき、集合 $A,B$ は等しいといい、$A=B$と書く。そうでないとき $A \ne B$ と書く。また $A \subset B $ かつ $ A \ne B$ のとき $A$ は $B$ の真部分集合であるといい、$A \subsetneq B$ と書く。
包含関係の記法にいくつかの流儀があるので、上記以外の代表的な書き方をふたつ紹介する。はじめにきちんと説明されていたり、文脈で判断できることが多いのでそれほど混乱することもないと思われる。- 数の不等号 $\lt$、$\leq$ にならって、 $A$ が $B$ の真部分集合のときのみ $A \subset B$ と書き、等号を含む場合は $A \subseteq B$ と書く。
- 真部分集合のときは $A \subsetneq B$ と書き、等号を含むときは $A \subseteq B$ と書く。
- 集合の中身をあらわす方法は次の $2$ つ
- 具体的に元を書き並べる
$X = \{ a,b,c,d,e \}$
（集合は「あるもの」がその集合の要素であるかどうかだけを気にするので、要素を書く順番や何回書かれているかは問わない。$\{ a,b,c,d,e \}$ と $\{ c,e,a,d,a,b \}$ は集合として同じものとみなす）
$Y = \{ 1,2,3 \ldots \}$ （元の数が無限個でも良い）
$Z_1 = \{ a,b,c \}$ 、$Z_2 = \{a,Z_1, \{ b,c \} \}$ （集合の中に集合があってもよいし、要素と集合が混在していてもよい） - 「 $|$ 」 の右側に要素の条件を記述する
$X= \{ x \,|\, x$ は $5$ 以上の自然数 $\}$
$Y= \{ x \in \mathbb{R} \,|\, 2 \leq x \lt 5 \}$
（要素の前提条件を「 $|$ 」の左側に書いてもよい。この場合、 $\mathbb{R}$ は実数全体の集合をあらわし（後述）、$Y$ は「$2$ 以上 $5$ 未満の実数をすべて集めた集合」をあらわす）
- 具体的に元を書き並べる
- 数の集合はよく使われるので、標準的な記号がある
$\mathbb{N}$ ： 自然数全体の集合 $= \{0,1,2,3 \ldots \}$（自然数に $0$ を入れないことも多いので文献ごとに確認すること）
$\mathbb{Z}$ ：整数全体の集合 $= \{0, \pm 1, \pm 2,\pm 3 \ldots \} $
$\mathbb{Q}$ ：有理数全体の集合 $= \{ \frac{a}{b} \,| a,b \in \mathbb{Z} かつ b \ne 0 \}$
$\mathbb{R}$ ：実数全体の集合
$\mathbb{C}$ ：複素数全体の集合 $= \{ a+bi \,| a,b \in \mathbb{R}\}$ （ただし $i^2 = -1$ とする。）
包含関係を書くともちろん、$ \mathbb{N} \subset \mathbb{Z} \subset \mathbb{Q} \subset \mathbb{R} \subset \mathbb{C}$ が成り立つ。
集合の演算、集合族、空集合
- 集合に対して次の演算は基本的である。
- 集合 $A,B$ に対して、$A \cap B = \{ x \,|\, x \in A かつ x \in B\}$ （「$A$ と $B$ の共通部分」あるいは「$A$ キャップ $B$」と読む）
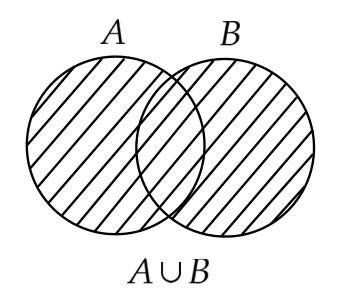
- 集合 $A,B$ に対して、$A \cup B = \{ x \,|\, x \in A または x \in B\}$ （「$A$ と $B$ の和集合」あるいは「$A$ カップ $B$」と読む）
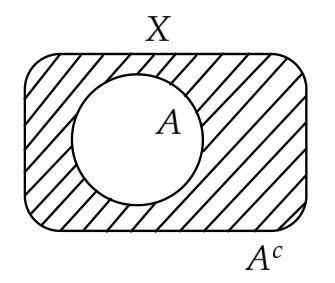
- $X$ を集合、$A$ を $X$ の部分集合とするとき、$A^{c} = \{ x \in X \,|\, x \notin A \}$ （「$A$ の補集合」と読む。 $\overline{A}$ とも書く ）
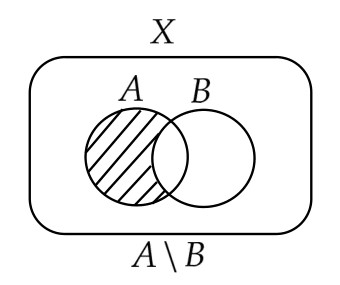
- $X$ を集合、$A$、$B$ を $X$ の部分集合とするとき、$A \setminus B= A \cap B^{c}$ （「$A$ から $B$ を引いた差集合」と読む）
- $I$ を集合とし、$i \in I$ ごとに集合 $X_i$ が与えられているとする。これらの集合をひとまとめにして考えたいとき、$\{ X_i \} _{i \in I}$ と書き、$I$ を添え字集合とする集合族という。添え字集合によっては次のように書くこともある。
- $I$ が有限集合 $I = \{ 1,2, \ldots , n \}$ のとき、$ \{ X_i \}_{i=1}^{n}$
- $I=\mathbb{N}$ （自然数の集合）のとき、$\{ X_i \}_{i=0}^{\infty}$
- いちいち書く必要がないくらい添え字集合が明らかなとき、$\{ X_i \}$
- 集合の「和集合をとる操作」は結合律をみたす。つまり、 $A$、$B$、$C$ を集合とすると
$$ (A \cup B )\cup C = A \cup (B \cup C )$$ が成立する（下の「基本的な性質」参照）。したがって、「和集合をとる操作」はかっこの付け方によらないので、先ほどの式はかっこを省略して $A \cup B \cup C$ と書いてよい。一般的に、有限個からなる集合族 $\{ A_i\}_{i=1}^n$ の和集合はかっこの付け方によらない（数学的帰納法による）。これを $\bigcup _{i=1}^{n} {A_i}$ と書く。つまり、 $$ \bigcup _{i=1}^{n} {A_i} = A_1 \cup A_2 \cup \ldots \cup A_n = \{ x \,|\, ある i =1,2, \ldots ,n が存在して x \in A_i \} $$ である。「共通部分をとる操作」も同様に考えて $$ \bigcap _{i=1}^{n} {A_i} = A_1 \cap A_2 \cap \ldots \cap A_n =\{ x \,|\, 任意の i =1,2,\ldots,n に対して x \in A_i\} $$ と書くことができる。
- 上記の有限個の和集合、共通部分を踏まえて、一般の和集合、共通部分を次のように定義する。
$I$ を添え字集合、$\{ A_i \} _{i \in I}$ を集合族とするとき、 $$ \bigcup _{i \in I} {A_i} = \{ x \,|\, ある i \in I が存在して x \in A_i \} $$ および、 $$ \bigcap _{i \in I} {A_i} = \{ x \,|\, 任意の i \in I に対して x \in A_i\} $$ と定義する。
- 要素を持たない集合を空集合といい、$\emptyset$ または $\{\}$ と書く。
$x \in \emptyset$ は $x$ にかかわらず常に偽なので、命題「$ x \in \emptyset \Rightarrow x \in A $」は集合 $A$ によらず常に真。よって任意の集合 $A$ に対して $\emptyset \subset A$ である。
集合の直積、直和
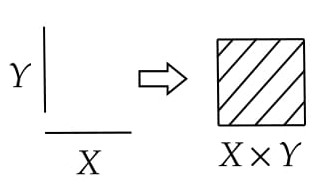
- $X$、$Y$ を集合とする。$X$ と $Y$ の元を（順序を区別して）並べた組全体
$$ X \times Y = \{ (x,y) \,|\, x \in X , y \in Y \} $$ を$X$ と $Y$の直積という。直積のふたつの元 $(a,b)$、$(c,d)$ は「$a=c$ かつ $b=d$」のとき等しいと定める。直積の組 $( , )$ は順序を区別しているので一般的には $(x,y) \ne (y,x)$ である。
- $n$ 個の集合 $X_1 , X_2 , \ldots , X_n$ の直積も同様に定義する。つまり、
$$ X_1 \times X_2 \times \ldots \times X_n = \{ (x_1 , x_2 , \ldots , x_n) \,|\, x_1 \in X_1 , x_2 \in X_2 , \ldots , x_n \in X_n \} $$ と定義し、この直積の2つの元 $(x_1 , x_2 , \ldots , x_n)$、$(y_1 , y_2 , \ldots , y_n)$ は「任意の $i = 1,2,\ldots,n$ に対して $x_i= y_i$」であるとき等しいとする。
- もっと一般に、 $I$ を添え字集合、$\{ X_i \} _{i \in I}$ を集合族とするとき、一般の直積を
$$ \prod_{i \in I} X_i = \{ (x_i)_{i \in I} \,|\, 任意の i \in I に対して x_i \in X_i \} $$ と定義する。もちろんこの直積のふたつの元 $(x_i)_{i \in I}$ 、$(y_i)_{i \in I}$ は、任意の $i \in I$ に対して $x_i =y_i$ が成り立つとき等しいと定める。
- $X$、$Y$ を集合とする。$X \cap Y = \emptyset$ のとき、和集合 $X \cup Y$ は特に $X$ と $Y$ の直和であるという。
- $n$ 個の集合 $X_1 , X_2 , \ldots , X_n$ の直和も同様に定義する。つまり、「任意の $i,j = 1,2,\ldots,n$ に対して $i \ne j \Rightarrow X_i \cap X_j =\emptyset$」のとき和集合 $\bigcup_{i=1}^{n} X_i$ は $X_1 , X_2 , \ldots , X_n$ の直和であるという。
具体例
- $X= \{ 1,2,3,4,5\}$ 、$A= \{1,2,3 \}$ 、$B= \{ 3,4 \}$ とする。（このように今考えている範囲全体の集合 $X$ を全体集合という）
このとき、$A \cap B = \{ 3 \}$ 、$A \cup B = \{ 1,2,3,4 \}$ 、$A^{c} = \{ 4,5 \} $ なので、$1 \in A \cup B$ 、$2 \notin A^{c}$ である。
- 実数 $\mathbb{R}$ の区間を次のように定義する。$a,b \in \mathbb{R},a \lt b$ に対して、
- $(a,b)= \{x \in \mathbb{R} | a \lt x \lt b \}$ （開区間）
- $(-\infty,a)= \{ x \in \mathbb{R} | x \lt a \}$ （有界でない開区間、$(a,\infty)$ も同様に定義する）
- $[a,b]= \{x \in \mathbb{R} | a \leq x \leq b \}$ （閉区間）
- $[a,b)= \{x \in \mathbb{R} | a \leq x \lt b \}$ （半開区間、$(a,b]$ も同様に定義する）
開区間と閉区間の違いは端の有無だけであるが、その差が非常に重要な違いとなってくる（例えば閉区間 $[a,b]$ で定義された数列がある実数 $\alpha$ に収束したとすると、$\alpha \in [a,b]$ が成り立つ。しかし開区間では一般にこのようなことは成り立たない）。開区間、閉区間の概念を一般の集合に拡張したのが位相空間における開集合、閉集合である。
- $X$ を集合族とする。$X \times X$ の部分集合 $\{ (x,y) \in X \times X \,|\, x=y\}$ を $X$ の対角線集合という。
- 通常の $2$ 次元平面はふたつの実数の組であらわすことができるので、
$\mathbb{R} \times \mathbb{R} = \{ (x,y) \,|\, x,y \in \mathbb{R} \}$ と同一視する。通常 $\mathbb{R} \times \mathbb{R}$ を $\mathbb{R} ^{2}$ と書く。 同様に $3$ 次元空間は $\mathbb{R} ^{3} = \mathbb{R} \times \mathbb{R} \times \mathbb{R}$と同一視される。一般に $ \mathbb{R} ^{n} = \{ ( x_1 , x_2 , \ldots , x_n ) \,|\, x_i \in \mathbb{R} \}$ を考えることができ、これを$n$ 次元（実）ユークリッド空間という。
基本的な性質
$X$ を集合、$A,B,C$ を $X$ の部分集合とする。このとき以下が成立する。 Venn図を書いて納得することもできるが、定義に従ってきちんと証明することは先々必要なスキルであるので、ぜひ試みていただきたい。例えば、$A \subset B$ を証明するには「 $x \in A \Rightarrow x \in B$ 」を証明すればよく、$A=B$ を証明するには $A \subset B$ と $A \supset B$ を証明すればよい。
- $\emptyset \subset A$ （空集合はすべての集合の部分集合）
- $\emptyset ^{c} = X$
$X^{c} = \emptyset$ - $(A^{c})^{c} = A$
- $A \cap A^{c} = \emptyset$
$A \cup A^{c} = X$ - $A \subset A$ （反射律）
- 「 $A \subset B $ かつ $ B \subset C $ 」 $ \Rightarrow A \subset C$ （推移律）
- $A \cap B$ は「$A$ と $B$ に含まれる最大の $X$ の部分集合」である。
つまり、任意に $D \subset A $ かつ $ D \subset A$ となる $D \subset X$ をとってくると、$D \subset A \cap B$ が成り立つ。
- $A \cup B$ は「$A$ と $B$ を含む最小の $X$ の部分集合」である。
つまり、任意に $A \subset D $ かつ $ B \subset D$ となる$D \subset X$ をとってくると、$A \cup B \subset D$ が成り立つ。
- $A \cap A = A$
$A \cup A = A$ （べき等律） - $A \cap B = B \cap A$
$A \cup B = B \cup A$ （交換律） - $A \subset B \Leftrightarrow A \cap B = A$ （特に、$\emptyset \cap A = \emptyset$ ）
- $A \subset B \Leftrightarrow A \cup B = B$ （特に、$\emptyset \cup A = A$ ）
- $(A \cap B) \cap C = A \cap (B \cap C)$
$(A \cup B) \cup C = A \cup (B \cup C)$ （結合律） - $A \subset A \cup B$
- $A \cap B \subset A$
- $A \subset B \Leftrightarrow B^{c} \subset A^{c}$ （補集合は包含関係を逆にする）
- $A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$
$A \cup (B \cap C) = (A \cup B) \cap (A \cup C)$ （分配律） - $(A \cap B)^{c}= A^{c} \cup B^{c}$
$(A \cup B)^{c}= A^{c} \cap B^{c}$ （De Morganの定理） - 「 $A \subset B $ かつ $ A \subset C $ 」 $ \Rightarrow A \subset B \cap C$
- 「 $A \subset C $ かつ $ B \subset C $ 」 $ \Rightarrow A \cup B \subset C$
集合論の初歩
論理と命題 / 集合の基本的な用語、集合の演算 / 全称記号と存在記号 / 写像、像、逆像、写像のグラフ / 写像の合成、写像の拡大と制限 / 選択公理について / 単射、全射、全単射、逆写像 / 部分集合族、べき集合 / （ 演算と代数構造 ） / （ 関係、同値関係、商集合 ） / （ 初歩的な順序集合 ） / （ Zornの補題 ） / （ 集合の濃度 ）
