選択公理について
選択公理
$A_1 , A_2 , \ldots , A_n $ を空集合でない集合とする。つまり任意の $i=1,2,\ldots,n$ に対して各 $A_i$ は少なくともひとつは元を持つので、その元を例えば $a_i \in A_i$ と置く。集合 $A_i$ 達は有限個しかないので、すべての $A_i$ からひとつずつ元 $x_i \in A_i$ をとってくることは有限回の操作で実行可能である。したがって直積 $\prod_{i=1}^{n} A_i$ は元 $(a_i)_{i=1}^{n}$ を持つので $\prod_{i=1}^{n} A_i \ne \emptyset$ である。一方、$I$ を有限集合でない集合とし、無限個の空でない集合族 $\{A_i \} _{i \in I}$ を考える。もちろん個々の $i \in I$ に対して、$a_i \in A_i$ をひとつ取ってくることは、$A_i \ne \emptyset$ なので可能である。しかし「一斉に」$A_i$ 達の元をひとつずつ選んできて、$(a_i)_{i \in I} \in \prod_{i \in I} A_i$ とすることが(具体的なアルゴリズムを示したり、有限回の操作で実行したり)できるかどうかはまったく明らかではない。しかし、この操作を認めないと数学をする上で非常に不便であるため我々はこれを公理として承認する。すなわち次の性質を「選択公理 (axiom of choice)」として成り立つものとする。
定理 1 (選択公理)
$I$ を集合、 $\{ A_i \}_{i \in I}$ を集合族とする。このとき次が成り立つ。 $$ 「任意の i \in I に対して A_i \ne \emptyset 」 \Longrightarrow \prod_{i \in I} A_i \ne \emptyset $$
初歩的な応用例
ここでは写像に関する応用をひとつだけ説明し、残りは事実を列挙するにとどめる。
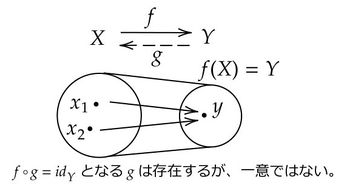
命題 2
$X$、$Y$ を集合とし、写像 $f \colon X \longrightarrow Y$ を考える。ただし、$f(X)=Y$ とする($f$ は全射であるという)。このとき、写像 $g \colon Y \longrightarrow X$ が存在して、$f \circ g = id_Y$ が成り立つ。
Proof.
(証明) $f(X)=Y$ なので、任意の $y \in Y$ に対して、$y \in f(X)$ が成り立つ。つまり、ある $x \in X$ が存在して $f(x)=y$ が成り立つ。ゆえに $x \in f^{-1}(y)$ である。以上から、任意の $y \in Y$ に対して、 $f^{-1}(y) \ne \emptyset$ が成り立つ。よって、選択公理より $\prod_{y \in Y} f^{-1}(y) \ne \emptyset$ なので $(x_y)_{y \in Y} \in \prod_{y \in Y} f^{-1}(y)$ が存在する。このとき $x_y \in f^{-1}(y)$ なので、$f(x_y)=y$ である。今、写像 $g \colon Y \longrightarrow X$ を $g(y)=x_y$ で定める($g$ は$(x_y)$ の取り方に依存する)。すると、任意の $y \in Y$ に対して、$f \circ g(y) = f(x_y) =y$ となる。以上から、$f \circ g = id_Y$ が成り立つ。この $g$ が求める写像であった。 (証明終わり)
□以下、未定義の用語を多用するが次のような結果も知られている。
- ('''zorn の補題''') 帰納的順序集合は極大元を持つ。
- $K$ を体とし、$V$ を $K$ 上のベクトル空間とする。$V$ が $0$ 以外の点を持つとき、$V$ は基底を持つ。
集合論の初歩
論理と命題 / 集合の基本的な用語、集合の演算 / 全称記号と存在記号 / 写像、像、逆像、写像のグラフ / 写像の合成、写像の拡大と制限 / 選択公理について / 単射、全射、全単射、逆写像 / 部分集合族、べき集合 / ( 演算と代数構造 ) / ( 関係、同値関係、商集合 ) / ( 初歩的な順序集合 ) / ( Zornの補題 ) / ( 集合の濃度 )