Globally Hyperbolic時空

globally hyperbolic時空は時空の中でも特に因果的な性質が良い時空のクラスである。 ここではglobally Hyperbolic時空についていくつかの有名な事実及びその証明を記載する1。 globally hyperbolic時空以外の時空の因果的なクラスや基本的な概念・用語については、因果階層を参照されたい。

＜＜執筆途中、完成率95%＞＞

globally hyperbolic時空が因果階層の中で一番狭い集合である。 この時空の性質は物理的に見て極めて自然な要請である。 またリーマン多様体におけるコンパクト多様体に類似の地位を占めておりLorentz幾何学において数学的にしばしば扱いやすい時空である。

Globally Hyperbolic時空の概要

ここではglobally hyperbolic時空や関連する概念の定義、およびいくつかの有名な定理についてまとめる。 証明は次の章を参照されたい。

定義 1 (globally hyperbolic時空)

時空 $(M,g)$ の部分集合 $H$ がglobally hyperbolic(大域双曲的)であるとは、(1) $H$ の全ての点がstrongly causalであり、(2) 任意の $p,q\in H$ に対して、$J(p,q):=J^+(p)\cap J^-(q)\subset H$ かつ $J(p,q)$ がコンパクトとなることである。 $H=M$ となるとき、$(M,g)$ がglobally hyperbolicであるという。

命題 2

globally hyperbolic時空はcausally simple時空である。

Proof.

任意の $p\in M$ に対して、$J^\pm(p)$ が閉であることを示せばよい。 $q\in \overline{J^+(p)}$ に対して、点列 $\{q_n\}$ で $q_n\rightarrow q$ かつ $q_n\in J^+(p)$ となるものを取ることが出来る。 $r\in I^+(q)$ に対して、$I^-(r)$ は $q$ の近傍であるから $\{q_n\}\in I^-(r)$ としてよい。 よって $\{q_n\}\in J^+(p)\cap J^-(r)$ であるからglobally hyperbolicの仮定より $q_n\rightarrow q\in J^+(p)\cap J^-(r)\subset J^+(p)$ である。 従って、$\overline{J^+(p)}\subset J^+(p)$ である。

□

上の命題の証明から分かるように、定義の条件(2)が成り立てば $J^\pm$ は閉である。 条件(1)を単にcausalとした場合でもcausally simple時空となりstrongly causal時空であることが分かる。 従って条件(1)はcausalでもstrongly causalでもどちらでもよい。 また論理的にはstrongly causalという条件は少し冗長であるからcausalとした方が経済的である。 しかし、多くの文献で条件(1)としてstrongly causalが採用されることが多い。

時空のあるachronalな位相的超曲面 $S$ 上で場の初期条件を定めた時、それが時間発展して $S$ より未来の時空領域の任意の点における場の値が一意的に定まるという状況は物理的にはごく自然なことである。 このような $S$ はCauchy超曲面と呼ばれ、globally hyperbolic時空の同値な特徴づけを与える有用な概念である。 まず依存領域の概念を以下のように定義する。

定義 3 (domain of dependence)

$(M,g)$ を時空として、$A$ をachronal部分集合とする。 $A$ のfuture domanin of dependence(未来依存領域)$D^+(A)$ とは、$M$ の点 $p$ で $p$ を通る全ての延長不可能な過去向き時間的曲線が $A$ と交わるという性質を満たすものの集合である。 past domanin of dependence $D^-(A)$ も過去と未来を入れ替えて同様に定義する。 $D(A):=D^+(A)\cup D^-(A)$ を $A$ のdomain of dependenceという。

$D^+(A)$ は $A$ の情報のみから古典論的に完全に予測し得る時空の領域である。 このような領域の“境界”が以下に定義するCauchy horizonである。

定義 4 (Cauchy horizon)

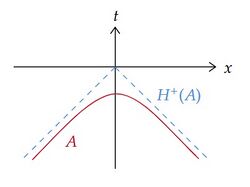
achronal集合 $A$ に対して、$A$ のfuture Cauchy horizon(未来Cauchy地平面) $H^+(A)$ は $H^+(A):=\overline{D^+(A)}\backslash I^-(D^+(A))$ と定義される。 past Cauchy horizon $H^-(A)$ も同様である。 $H(A):=H^+(A)\cup H^-(A)$ を $A$ のCauchy horizonと呼ぶ。

以下に定義するCauchy超曲面とはその集合の情報のみから古典論的に時空全体を完全に予測することのできるものである。

定義 5 (Cauchy超曲面)

時空 $(M,g)$ のCauchy超曲面とは次の同値な条件を満たす $M$ の部分集合 $S$ のことである。

(i) $M$ の任意の延長不可能なtimelike曲線は唯一点において $S$ と交わる。

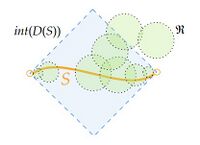
(ii) $S$ はachronalで $D(S)=M$.

(iii) $S$ はachronalで $H(S)=\emptyset$.

これら3つの条件が同値であることは自明ではない（証明は次節で与える）。 Cauchy超曲面 $S$ は次の性質を持つことが知られている。 $S$ は閉集合であり、位相的超曲面である。 $M=I^+(S)\coprod S\coprod I^-(S)$ である。 $S$ がspacelikeな場合は任意の延長不可能なcausal曲線と唯一点で交わる（このとき $S$ は少なくとも $C^1$ 級である）。 コンパクト集合 $K$ に対して、$J^\pm(K)\cap S$ はコンパクトである。 また関数 $t:M\rightarrow\mathbb{R}$ が ある $c\in\mathbb{R}$ に対して、$S=t^{-1}(c)$ を満たすとき $t$ はCauchyであるという。

次の定理はGerochにより示された顕著な結果である。

定理 6 (globally hyperbolic時空のCauchy超曲面による特徴づけ)

時空 $(M,g)$ がglobally hyperbolicであることとCauchy超曲面 $S$ を持つことは同値である。 さらにこのとき、Cauchy time functionが存在し、また任意のCauchy超曲面は $S$ と同相であり、$M$ は $S\times\mathbb{R}$ と同相である。

Globally Hyperbolic時空の種々の事実の詳細

ここでは先の章で紹介したものも含むGlobally Hyperbolic時空の種々の事実と証明を述べる。

基礎的な命題

ここではGlobally Hyperbolic時空に関する理論を展開するにあたり基礎的な役割を果たす命題を述べる。

補題 7

$(M,g)$ をstrongly causal時空とする。 $p,q\in M$ に対して、$p<q$ かつ $J(p,q):=J^+(p)\cap J^-(q)$ がコンパクトであるとする。 このとき、$p$ から $q$ へのcausal測地線 $\lambda$ で $L(\lambda)=\tau(p,q)<\infty$ となるものが存在する。

Proof.

$p<q$ であるから、$J(p,q)$ に含まれるcausal曲線の列 $\{\alpha_n\}$ で $L(\alpha_n)\rightarrow \tau(p,q)$ となるものが存在する（これは $p<q$ であるときは常に成り立つが、一般には $J(p,q)$ はコンパクトとは限らず、$\tau(p,q)<\infty$ とは限らない）。 今 $J(p,q)$ はコンパクトなので、因果階層の命題38より、有限個の折点を持つ区分的滑らかな測地線 $\lambda$ で $\lim_{n\rightarrow\infty}L(\alpha_n)\le L(\lambda)<\infty$ となるものが存在する。 従って、$L(\lambda)=\tau(p,q)<\infty$ である。

□

補題 8

$U$ をglobally hyperbolicな開集合とする。 このときtime separation $\tau|_U:U\times U\rightarrow\mathbb{R}_{\geq0}$ は連続である。

Proof.

背理法で示す。 $(p,q)\in U\times U,\ (p<q)$ において、$\tau$ が上半連続でないとする（time separationは常に下半連続である）。 上の命題より $\tau$ は有限である。 このとき、ある $\delta>0$ に対して、$p_n\rightarrow p,\ q_n\rightarrow q$ で $\tau(p_n,q_n)>\tau(p,q)+\delta$ となる点列 $\{p_n\},\{q_n\}$ が存在する。 $U$ はglobally hyperbolicであるから、各 $n$ に対して、$p_n$ から $q_n$ へ向かうcausal曲線 $\alpha_n$ で $L(\alpha_n)>\tau(p_n,q_n)-1/n$ となるものが存在する。 $U$ は開集合であるから、$q<q^+,\ p^-<p$ となる $p^-,q^+\in U$ が存在するから、$p_n,q_n\in J(p^-,q^+)$ としてよい（従って $\alpha_n\subset J(p^-,q^+)$）。 因果階層の命題38と上の補題7より、$p$ から $q$ へ向かうcausal測地線 $\lambda$ で $L(\lambda)\geq\lim L(\alpha_n)$ となるものが存在するから、$L(\lambda)\geq\lim L(\alpha_n)>\tau(p,q)+\delta$ となり $\tau(p,q)$ の極大性に矛盾する。

□

補題 9

$U$ をglobally hyperbolicな開集合とする。 このとき因果的関係「$<$」は閉である、すなわち、点列 $\{p_n\},\{q_n\}$ を $p_n<q_n,\ p_n\rightarrow p,\ q_n\rightarrow q$ となるものとするとき、$p<q$ が成り立つ。

Proof.

点列 $\{p_n\},\{q_n\}$ を $p_n<q_n,\ p_n\rightarrow p,\ q_n\rightarrow q$ となるものとし、$\{\alpha_n\}$ を $p_n$ から $q_n$ へのcausal曲線とする。 適当な $p'<p,\ q<q'$ に対して、$\alpha_n\subset J(p',q')$ としてよい。 Globally hyperbolicであるから、$J(p',q')$ はコンパクトである。 よって因果階層の命題38より、$p$ から $q$ への長さが有限の区分的滑らかなcausal測地線が存在する（$\{\alpha_n\}$ の擬極限として得られる）。 従って、$p<q$ である。

□

Achronal集合

Globally hyperbolic時空を論じるにあたってCauchy超曲面は非常に重要な概念である。 Cauchy超曲面はこの節で述べるAchronal集合の一種である。 この節ではAchronal集合の一般的な性質を述べる。

定義 10

部分集合 $A\subset M$ がachronal (resp. acausal)とは、$A$ の任意の2点がtimelike曲線 (resp. causal曲線) で結ばれないことである。

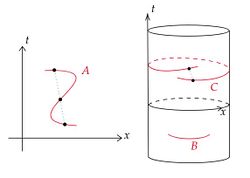
下図はachronalでない集合とachronal集合の例である。 集合A、Cはachronalでない。 特にCはspacelikeだがachronalでない。 このように時空が単連結でない場合はspacelike超曲面でもachronalとは限らない。 集合Bはachronalである。

時空の開集合はその中にtimelike曲線を含むので明らかにachronal集合ではない。 このことからachronal集合は“薄い”集合で“超曲面”のようなものであることが期待される。 光円錐はacrhonal集合であるが、頂点は滑らかでない。 このことからachronal集合は必ずしも滑らかではないことが分かる。 滑らかでない点を許す“超曲面”を正確に述べた概念は位相的超曲面と呼ばれる。 またachronal集合にはedgeという概念が定義される。 この節ではachronal集合に関して位相的超曲面であることとedgeの存在との関係について記載する。

定義 11

$A$ をachronal集合とするとき、$edg(A)$ とは $\bar{A}\ni p$ で「$p$ の任意の近傍 $U$ は $I^-(p,U)$ から出て $I^+(p,U)$ に達するtimelike曲線で $A$ と交わらないものを含む」という性質を満たす点の全体である。 $edg(A)$ は $A$ のedgeと呼ばれる。

例 12 (achronal集合のedgeの例)

2次元Minkowski時空 $\mathbb{E}^{(1,1)}$ においてachronal集合 $A_1:=\{(0,x)\in\mathbb{E}^{(1,1)};\ x\in\mathbb{R}\}$ に対しては、$edg(A_1)=\emptyset$ である。 また $A_2:=\{(0,x)\in\mathbb{E}^{(1,1)};\ -1\le x<1\}$ に対しては、$edg(A_2)=\{(0,\pm1)\}$ であり、$A\cap edg(A)=\{(0,-1)\}$ である。 3次元Minkowski時空 $\mathbb{E}^{(1,2)}$ においてspacelikeな超平面 $\Pi$ はachronal集合である。 $p\in\Pi$ に対して、$A_3:=\Pi-\{p\}$ もachronal集合であり、$p$ を通る任意のtimelike曲線は $A_3$ と交わらないから $edg(A_3)=\{p\}$である。

上の $A_3$ の例は一般的な言明にすることができる。 すなわち、achronal集合 $A$ に対して、$\bar{A}-A\subset edg(A)$ である。 なぜならもし $p\in\bar{A}-A$ を通るtimelike曲線が $A$ と点 $q$ で交わるなら $p,q$ それぞれの適当な近傍の点はtimelike曲線で結ばれるため（chronologicalという因果関係は開であるという一般的な性質より） $A$ がachronalであることに矛盾するからである。

定義 13

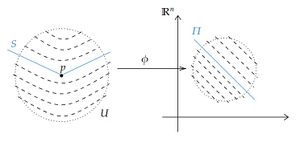
多様体 $M$ の部分集合 $S$ が位相的超曲面であるとは、$p\in S$ に対して、ある近傍 $U(\ni p)$ と中への同相写像 $\phi:U\rightarrow\mathbb{R}^n$ と適当な $\mathbb{R}^n$ の超平面 $\Pi$ で $\phi(U\cap S)=\phi(U)\cap\Pi$ となるものが存在するときをいう。

例 14 (位相的超曲面の例)

2次元Minkowski時空 $\mathbb{E}^{(1,1)}$ において $S_1:=\{(0,x)\in\mathbb{E}^{(1,1)};\ x\in\mathbb{R}\}$ は位相的超曲面である。 また $S_2:=\{(0,x)\in\mathbb{E}^{(1,1)};\ |x|<1\}$ も位相的超曲面である。 $S_3:=\{(0,x)\in\mathbb{E}^{(1,1)};\ |x|\le1\}$ は位相的超曲面でない。 なぜなら $\{(0,\pm1)\}$ に対しては、上記の定義における $U,\phi$ は取れないからである。

命題 15

achronal集合 $A$ が位相的超曲面であることと、$A\cap edg(A)=\emptyset$ であることは同値である。

Proof.

$A$ が位相的超曲面であるとする。 $p\in A$ の近傍 $U$ で位相的超曲面の定義の条件を満たすものを取ると $A-U$ は2つの連結成分を持つ。 $A$ がachronalであるから $I^-(p,U)$ と $I^+(p,U)$ は交わりを持たず、開集合で $A$ とも交わらない。 さらに $p$ を通る任意のtimelike曲線は $I^-(p,U)$ と $I^+(p,U)$ の両方と交わるからそれぞれ $A-U$ の別の連結成分に含まれる。 よって $I^-(p,U)$ から $I^+(p,U)$ へ至る任意のtimelike曲線は $A$ と交わる。 $p$ の任意の近傍は $U$ と交わりを持つから、$p\notin edg(A)$ である。 従って、$A\cap edg(A)=\emptyset$ である。

$A\cap edg(A)=\emptyset$ とする。 任意の $p\in A$ に対して、$p$ の凸近傍を $C$ とする。 $\mathbb{R}^{n-1}$ の開集合 $\widetilde{N}$ と $a,b,\delta\in \mathbb{R}$ に対して $\widetilde{V}=I\times \widetilde{N}$ と定義する。 ただし、$I=\{t\in\mathbb{R};\ a-\delta\le t\le b+\delta\}$ である。 必要なら $\widetilde{N},a,b,\delta$ を適当に取り直すことで、$\exp(\widetilde{V})=V\subset C$ かつ $\exp(\{t=a\}\times \widetilde{N})\subset I^-(p,C),\ \exp(\{t=b\}\times \widetilde{N})\subset I^+(p,C)$ が成り立つとしてよい。 また $d\exp(\partial_t)$ は至る所timelikeであるとしてよい。

これ以降 $\exp$ を通じて $V$ と $\widetilde{V}$ を同一視する。 また $N=\exp(\{t=0\}\times \widetilde{N})$ とする。 $t$ のみ動かして出来る $t-$曲線はtimelike曲線である。 $A$ はachronalであり、かつ $p\in edg(A)$ でないから、必要なら $C$ を小さく取り直せば、各 $t$ 曲線は $a-\delta\le t\le b+\delta$ の範囲において $A$ と唯一点で交わる。 従って、関数 $h:N\rightarrow\mathbb{R}$ があり、$A\cap V=\{(t,x)\in V;\ t=h(x),\ x\in N\}$ となる。

次に $h:N\rightarrow\mathbb{R}$ が連続であることを示す。 点列 $\{y_n\}\in N$ に対して、$y_n\rightarrow y\in N$ かつ $\lim_nh(y_n)\ne h(y)$ となっているとする。 $h(y_n)\in I$ であり、 $I$ はコンパクトであるから、収束する部分列 $h(y_m)\rightarrow r\ne h(y)$ が存在する。 $q=(h(y),y)\in A\cap V$ と置く。 $\partial_t$ はtimelikeであり、$q$ と $(r,y)$ は同じ $t-$曲線上にあるから、$(r,y)\in I^+(q,V)\cup I^-(q,V)$ である。 $q_m=(h(y_m),y_m)$ と置く。 $I^+(q,V)\cup I^-(q,V)$ は $(r,y)$ の近傍であるから $\{q_m\}\in I^+(q,V)\cup I^-(q,V)$ である。 $q_m,q\in A$ であるから $A$ がachronalであることに矛盾する。

最後に、$I$ を $t\mapsto t-h(x)$ とする微分同相を考えると、$A$ が位相的超曲面であることが分かる。

□

この命題から直ちに次の系を得る。

系 16

$A$ をachronal集合とするとき、 $A$ が閉位相的超曲面であることと、$edg(A)=\emptyset$ であることは同値である。

未来集合・過去集合

因果的未来（因果的過去）を取る操作について閉じている集合を未来集合（過去集合）という。 その境界はachronalな閉位相的超曲面となるという顕著な性質がある。

定義 17

時空 $(M,g)$ の部分集合 $F$ が未来集合 (future set) であるとは、$I^+(F)\subset F$ となることである。 過去集合も未来と過去を入れ替えて同様に定義する。

例えば任意の部分集合 $U$ に対して、$I^+(U)$ は未来集合である。

命題 18

未来集合 $F$ の境界 $\partial F$ はachronalな閉位相的超曲面である。

Proof.

初めに次の単純な補題を示す。

補題

$F$ が未来集合ならば、$M-F$ は過去集合である。

Proof.

もし $I^-(M-F)\subset M-F$ でないならば、$I^-(M-F)\cap F\ne\emptyset$ であり、$I^+(F)\cap(M-F)\ne\emptyset$ となり、$F\cap(M-F)\ne\emptyset$ となるから矛盾する。

□

次にこの補題を使い $\partial F$ がachronalであることを示す。 そのためには、$I^+(\partial F)\cap I^-(\partial F)=\emptyset$ を示せば良い。 $p\in\partial F=\bar{F}-int(F)$ とする。 任意の $q\in I^+(p)$ に対して、$I^-(q)$ は $p$ の開近傍であるから、 $I^-(q)\cap F\ne\emptyset$ である。 よって $q\in I^+(F)\subset F$ であるから、$I^+(p)\subset F$ である。 同様に、$I^-(p)\subset M-F$ である。 これより、$I^+(\partial F)\cap I^-(\partial F)=\emptyset$ が分かる。

系16より $edg(\partial F)=\emptyset$ を示せば証明が完了する。 上の証明より、任意の $p\in\partial F$ に対して、$I^+(p)\subset int (F),\ I^-(p)\subset ext(F)$ である。 さらに $M=\bar{F}\coprod(M-\bar{F})=int F\coprod\partial F\coprod ext(F)$ である。 よって $I^-(p)$ から $I^+(p)$ へ至るtimelike曲線は必ず $\partial F$ と交わる。 よって $\partial F$ はedgeを含まない。

□

Cauchy超曲面

Cauchy超曲面はGlobally hyperbolic時空を論じる上で決定的に重要な概念である。

定義 19

時空 $(M,g)$ の部分集合 $S$ がCauchy超曲面であるとは、$M$ の任意の延長不可能なtimelike曲線が $S$ と唯一点で交わるときをいう。

定義よりCauchy超曲面はachronalであることが分かる。 より強く次が成り立つ。

命題 20

Cauchy超曲面はachronalな閉位相的超曲面である。

Proof.

Cauchy超曲面を $S$ とする。 $M=I^+(S)\coprod S\coprod I^-(S)$ である。 $\overline{I^+(S)}\supset S$ である。 さらにもし $\overline{I^+(S)}\cap I^-(S)\ne\emptyset$ なら $I^-(S)$ は開集合であるから、$I^+(S)\cap I^-(S)\ne\emptyset$ となり $S$ がcauchy超曲面であることに矛盾する。 従って、$\overline{I^+(S)}\cap I^-(S)=\emptyset$ である。 同様に、$I^+(S)\cap \overline{I^-(S)}=\emptyset$ である。 従って、$\partial I^+(S)=\partial I^-(S)=S$ である。 $I^+(S)$ は未来集合であるから、$S=\partial I^-(S)$ はachronalな閉位相的超曲面である。

□

次の補題はしばしばCauchy超曲面や次節の依存領域を論じる上でしばしば有用である。

補題 21

$\alpha:[0,\infty)\rightarrow M,\ \alpha(0)=p$ を過去向きの延長不可能なcausal曲線とし、閉集合 $C$ で $C\cap\alpha=\emptyset$ となるものが存在するとする。 このとき、任意の $p_0\in I^+(p,M-C)$ に対して、$p_0$ から出る過去向き延長不可能なtimelike曲線 $\beta$ で、$\beta\cap C=\emptyset$ となるものが存在する。 ただし、写像 $\alpha:I\rightarrow M$ の 像 $\alpha(I)$ も $\alpha$ と書いた。

Proof.

開部分リーマン多様体 $(M\backslash C,g|_{M\backslash C})$ で考える。 $\alpha(0)<<p_0$ かつ $\alpha(1)\le\alpha(0)$ であるから、$\alpha(1)<<p_0$ である。 従って、$\alpha(1)<<p_1<<p_0$ となる $p_1$ が存在する。 同様に $k\geq1$ に対して、$\alpha(k+1)<<\alpha(k),\ \alpha(k)<<p_k$ のとき $\alpha(k+1)<<p_k$ であるから、$\alpha(k+1)<<p_{k+1}<<p_k$ となる $p_{k+1}$ が存在する。 各 $p_n$ を $\alpha(n)$ の十分近くに取ることが出来るので $\{p_n\}$ を結ぶ延長不可能なtimelike曲線で $M\backslash C$ に含まれるものが得られる。

□

定義よりCauchy超曲面は任意の延長不可能なtimelike曲線と唯一点で交わるが、実はcausal曲線とも交わることを主張するのが次の命題である。 ただし、唯一点で交わるとは限らない。

命題 22

Cauchy超曲面は任意の延長不可能なcausal曲線と交わる。

Proof.

Cauchy超曲面を $S$ とする。 $S$ と交わらないcausal曲線 $\alpha$ が存在するとする。 $S$ は閉集合であるから、上の補題より $S$ と交わらない延長不可能なtimelike曲線が存在し、$S$ がCauchy超曲面であることに矛盾する。

□

時空 $(M,g)$ は定義より時間的向き付け可能で、従ってtimelikeベクトル場が存在する。 timelikeベクトル場 $X$ が与えられたとする。 Cauchy超曲面 $S$ が存在すれば、$X$ の全ての極大積分曲線は延長不可能なtimelike曲線であるから、$S$ と唯一点で交わる。 任意の $p\in M$ に対して、$p$ を通る $X$ の極大積分曲線と $S$ との交点を $\rho(p)$ とすると、写像 $\rho:M\rightarrow S$ が定義される。 このとき、次が成り立つ。

命題 23

$\rho:M\rightarrow S$ は連続・全射な開写像である。

Proof.

ベクトル場 $X$ の生成する1パラメータ変換群を $\Psi:\mathbb{R}\times M\supset D\rightarrow M$ ($D$ は開集合) とする。 常微分方程式の初期条件に関する解の連続性の定理から、$\Psi$ は連続である。 $D(S):=(\mathbb{R}\times S)\cap D$ は $D$ の位相的超曲面であるから、$D(S)$ は位相多様体であり、次元は $M$ と同じである。 さらに $\Psi|_{D(S)}:D(S)\rightarrow M$ は連続かつ全単射である。 ここで代数トポロジーでよく知られた定理invariance of domainを使う。

補題 24

$U$ を $\mathbb{R}^n$ の開集合とし、$f:U\rightarrow\mathbb{R}^n$ を連続な単射とする。 このとき、$f(U)$ は $\mathbb{R}^n$ において開集合である。

これより、$\Psi|_{D(S)}$ の逆写像も連続となり、位相同相写像となる。 射影を $\pi:\mathbb{R}\times S\rightarrow S$ とすれば、$\pi$ は連続かつ開写像である。 従って、$\rho=\pi\circ\Psi|_{D(S)}^{-1}$ も連続かつ開写像である。

□

これより次のCauchy超曲面に関する顕著な系が得られる。

系 25

時空 $(M,g)$ が2つのCauchy超曲面を持つとき、その2つのCauchy超曲面は同相である。

Proof.

2つのCauchy超曲面を $S,T$ とする。 timelikeベクトル場を一つ選び、それに関する $S,T$ への射影を $\rho_T,\rho_S$ とする。 Cauchy超曲面の性質から明らかに $\rho_T,\rho_S$ は互いに逆写像であるから、位相同相写像である。

□

依存領域

依存領域は時空における場の因果的発展を論じる上で決定的に重要な概念である。 さらにCauchy超曲面が存在するときGlobally hyperbolic時空であることの証明に有用である。

定義 26

$A$ をachronal集合とするとき、 $$ D^+(A):=\{p\in M;\ pを通る任意の過去向きの延長不可能なcausal曲線がAと交わる\} $$ を $A$ のfuture domain of dependence (未来依存領域) という。 past domain of dependence (過去依存領域) $D^-(A)$ も同様に定義する。 $D(A)=D^+(A)\cup D^-(A)$ を $A$ のdomain of dependence (依存領域) という。

命題 27

時空 $(M,g)$ のachronal集合 $A$ がCauchy超曲面であることと $D(A)=M$ となることは同値である。

Proof.

$A$ がCauchy超曲面なら明らかに $D(A)=M$ である。 逆に $D(A)=M$ とすれば、$M$ の延長不可能なtimelike曲線で $A$ と交わらないものは存在せず、achronalよりただ1点で交わる。 $\square$

□

定理 28

achronal集合 $A$ に対して、$int D(A)$ はGlobally hyperbolicである。

Proof.

初めに頻繁に使う補題を示す。

補題 29

$A$ を任意のachronal集合とするとき、任意の $p\in int(D(A))$ を通る任意の延長不可能なcausal曲線は $I^-(A),\ I^+(A)$ と交わる。

Proof.

$p\in (A\cup I^+(A))\cap int(D(A))$ とする。 $\alpha$ を $p$ から出る過去向きの延長不可能なcausal曲線とする。 補題21の証明から分かるように、$p_0\in I^+(p,int(D(A)))$ を通る過去向きの延長不可能なcausal曲線 $\beta:[0,\infty)\rightarrow M$ で任意の $s\in[0,\infty)$ に対して、$I^-(\beta(s))\cap\alpha\ne\emptyset$ となるものが存在する。 $\beta$ は $A$ と交わるから $\alpha$ は $I^-(A)$ と交わる。 $I^+(A)$ も同様である。 $\square$

□

以下の4Stepに別けて証明する。

Step1 : $int(D(A))$ はcaualである。

Proof.

もし $int(D(A))$ がcausalでないとすると、閉causal曲線 $\gamma$ が存在する。 必要ならパラメータを取り直すことで延長不可能なcausal曲線 $\tilde{\gamma}$ に延長することができる（無限回同じ閉曲線を回るようにすればよい）。 $D(A)$ の定義より $\tilde{\gamma}$ は $A$ と交わり、また上の補題より $I^\pm(A)$ とも交わる。 $\tilde{\gamma}$ はcausalであるから、$\tilde{\gamma}\subset I^\pm(A)$ である。 $\tilde{\gamma}(t_1),\tilde{\gamma}(t_2)\in A$ かつ $\tilde{\gamma}(t_1)<\tilde{\gamma}(t_2)$ であるとする。 $\tilde{\gamma}\subset I^+(A)$ なので $\tilde{\gamma}(t_2)\in I^+(A)$ である。 よって $\tilde{\gamma}(t_1)<<\tilde{\gamma}(t_2)$ であるからAがachronalであることに矛盾する。 $\square$

□

Step2 : $int(D(A))$ はStrongly causalである。

Proof.

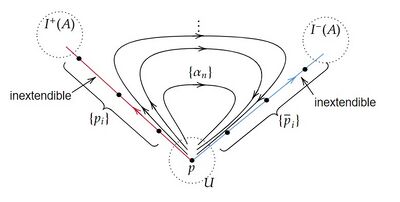
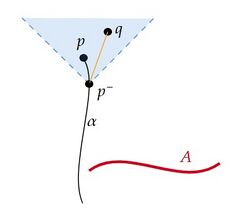
$p\in int(D(A))$ がstrongly causalではないと仮定して矛盾を導く。 $p$ の任意の近傍 $U$ に対して、未来向きcausal曲線の族 $\{\alpha_n\}:[0,1]\rightarrow M$ で $\alpha_n(0),\alpha_n(1)\rightarrow p$ となり $U$ に含まれないものが取れる。 $\{p_i\}$ を $\{\alpha_n\}$ の極限点列とする。 もし $\{p_i\}$ が有限列ならば、$p=p_0<p_1<\cdots<p_k=\lim_n\alpha_n(1)=p$ であるから、$p<p$ となりStep1の結論に矛盾する。 従って、$\{p_i\}$ は無限列であり、擬極限曲線 $\lambda$ は未来向きの延長不可能なcausal曲線である。 Step1の補題より、$\lambda$ は $I^+(A)$ と交わる。 従って、ある $j$ があり、$p_j\in I^+(A)$ としてよい。 このとき、ある $s_{m,j}\in[0,1]$ があり、$\lim_m\alpha_m(s_{m,j})=p_j$ となる。 次に、$\alpha_n|_{[s_{n,j},1]}$ のパラメータを逆向きにして過去向きのcausal曲線 $\bar\alpha_n:[0,1-s_{n,j}]\rightarrow M$ の族を考える。 上と同様に $\{\bar\alpha_n\}$ の極限点列 $\{\bar{p}_i\}$ は無限列であり、擬極限曲線 $\bar{\lambda}$ は過去向きの延長不可能なcausal曲線であり、$I^-(A)$ と交わる。 $\bar{p}_j\in I^-(A)$ とし、ある $\bar{s}_{m,j}\in[0,1]$ があり、$\lim_m\bar{\alpha}_m(\bar{s}_{m,j})=\bar{p}_j$ となるとする。 このとき、十分大きい $m$ があり、$\alpha_m(s_{m,j})\in I^+(A),\ \bar{\alpha}_m(\bar{s}_{m,j})\in I^-(A)$ となる。 よってある $a,\bar{a}\in A$ があり、$a<<\alpha_m(s_{m,j})<\bar{\alpha}_m(\bar{s}_{m,j})<<\bar{a}$ となるから $A$ がachronalであることに矛盾する。

(下図は証明の概念図である。赤色の曲線は極限点列 $\{p_i\}$ に対する擬極限曲線 $\lambda$を、青色の曲線は $\{\bar{p}_i\}$ に対する擬極限曲線 $\bar\lambda$ を表している。各 $\{\alpha_n\}$ は $U$ の点から出て未来向きに進むことで $U$ の点に戻ってくるが、$\lambda$ と $\bar\lambda$ は連結されていない。しかし $\lambda,\bar\lambda$ にいくらでも近い $\alpha_n$ は存在する。) $\square$

□

Step3 : 任意の $p,q\in int(D(A)),\ p\le q$ に対して、$J^+(p)\cap J^-(q)$ はコンパクトである。

Proof.

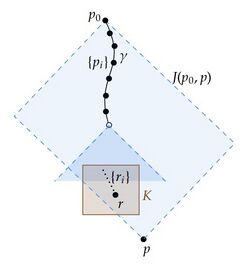
$p=q$ のときは明らかである。 $p<q$ のときを考える。 点列 $\{x_n\}\in J(p,q)$ が $J(p,q)$ に集積点を持つことを示せば良い。 $p$ から出て $x_n$ を通り $q$ へ至る未来向きのcausal曲線を $\alpha_n:[0,1]\rightarrow M$ とする。

$\{\alpha_n\}$ の極限点列が有限列のときを考える。 極限点列の作り方から極限点列 $\{p_i\}$ の隣接する2点に対して、それらを含む凸近傍を一つ取ることができる。 これらの凸近傍は有限個であるから、部分列 $\{x_m\}$ とある凸近傍 $C$ が存在して、$C\supset\alpha_m([s_{i-1,m},s_{i,m}])\ni x_m$ となる。 $C$ はある凸近傍に関して相対コンパクトであるから、必要ならさらに部分列を取り直して、$x_m\rightarrow x\in C$ となる。

次に $\{\alpha_n\}$ の極限点列が無限列のときを考える。 擬極限曲線 $\lambda$ は未来向きの延長不可能なcausal曲線であるから、Step1の補題より、$p_l\in\lambda\cap I^+(A)$ となるものがある。 従って、$\alpha_m(s_m)\rightarrow p_l(\ne q)$ とできる。 ここで、$\alpha|_{[s_m,1]}$ のパラメータを逆にした過去向きのcausal曲線 $\bar\alpha_m$ を考える。 曲線族 $\{\bar\alpha_m\}$ の極限点列 $\{\bar p_i\}$ が有限列となることはない（$\lambda$ が延長不可能であることに矛盾する）。 よって $\{\bar\alpha_m\}$ の擬極限曲線 $\bar\lambda$ は過去向きの延長不可能なcausal曲線であるから、$\bar\lambda\cap I^-(A)\ne\emptyset$ である。 従って、十分大きい $m$ があり、$\alpha_m\cap I^\pm(A)\ne\emptyset$ である。 よってStep2の最後の議論と同様に $A$ がachronalであることに矛盾する。 $\square$

□

Step4 : 任意の $p,q\in int(D(A)),\ p\le q$ に対して、$J^+(p)\cap J^-(q)\subset int(D(A))$ である。

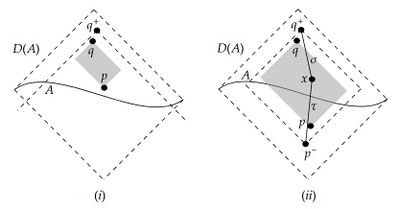
Proof.

(i) $p,q\in int(D^+(A))$ のとき $p<q$ とする。 $q<q^+$ となる $q^+\in int(D^+(A))$ を一つとる。 $D^+(A)$ の定義から開集合 $N:=I^+(A)\cap I^-(q^+)$ が $D^+(A)$ に含まれる。 よって、$J(p,q)\subset N\subset D^+(A)$ である。

(ii) $p\in int(D^-(A)),\ q\in int(D^+(A))$ のとき $p^-<p,\ q<q^+$ となる $p^-,q^+\in int(D(A))$ をとる。 $N:=I^+(p^-)\cap I^-(q^+)$ とする。 $N\subset D(A)$ を示せば良い。 任意の $x\in N$ に対して、$p^-$ から出て $x$ へ至る未来向きtimelike曲線を $\tau$、$x$ から出て $q^+$ へ至る未来向きtimelike曲線を $\sigma$ とする。 $x\in A$ ならば $x\in D(A)$ である。 $x\notin A$ のとき、$A$ がachronalであることから $\tau,\sigma$ の両方が $A$ と交わることもありえない。 $\tau$ が $A$ と交わるとき、$x\in I^+(A)$ である。 $x$ から出る過去向きの延長不可能なcaual曲線 $\beta$ に対して、$\sigma\cup\beta$ は $q^+$ から出る過去向きの延長不可能なcaual曲線であり、従って $A$ と交わる。 $\sigma$ は $A$ と交わらないから $\beta$ が交わる。 よって $x\in D^+(A)$ である。 $\sigma$ が $A$ と交わるときも同様に $x\in D^-(A)$ である。 従って、$J(p,q)\subset N\subset D(A)$ である。 $\square$

□

□

この定理において $D(A)$ の内点であるという仮定を外すことは出来ない。 下図において $A$ を赤色の線分（端点を含む）とすれば $D(A)$ の境界の点がstrongly causalでないということがあり得るからである。

系 30

Cauchy超曲面が存在するならばGlobally hyperbolicである。

Proof.

$S$ がCauchy超曲面ならば任意の $p\in M$ を通る延長不可能なtimelike曲線は定義より $S$ と交わる。 さらに$p\in M$ を通る延長不可能なcausal曲線は命題22より $S$ と交わる。 よって $D(S)=M$ であり、$int(D(S))=M$ であるから、上の定理より従う。 $\square$

□

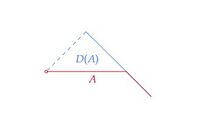
定理28において $D(A)$ が開集合の場合は内点という条件は外すことができる。 $A\cap edg(A)\ne\emptyset$ なら $D(A)$ は明らかに開集合にならないから、$D(A)$ が開集合となるためには $A$ が位相的超曲面となるべきである。 また下図の $A$ はachronalだがacausalではなく、このとき $D(A)$ は開集合とはならない。

これらのことから $D(A)$ が開集合となるための条件はacausalな位相的超曲面であると期待できる。 実際、次の命題が成り立つ。

命題 31

$S$ をacausalな位相的超曲面とすると $D(S)$ は開集合である。 従って $D(S)$ はglobally hyperbolicである。

Proof.

2つのStepに分けて証明する。

Step1.

補題 (1)

$S\subset int(D(S))$

Proof.

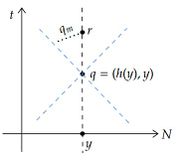
$p\in S-int(D(S))$ が存在したとして矛盾を導く。 $p\in\overline{ext(D(S))}$ であるから、点列 $\{p_n\}\notin D(S)$ で $\lim p_n=p$ となるものが存在する。 $S$ は $edg(S)$ を含まないから $I(S)=I^+(S)\cup S \cup I^-(S)$ は開集合である。 また $S\subset D(S)\subset I(S)$ であるから $\{p_n\}\in I^+(S)$ と仮定してよい。 さらに $\{p_n\}\notin D(S)$ より延長不可能な過去向きのcausal曲線の族 $\{\alpha_n\}:[0,b_n)\rightarrow M$ で $\alpha_n(0)=p_n$ かつ全ての $\alpha_n$ は $S$ と交わらないものが存在する。

$p$ の凸近傍 $C\subset I(S)$ を取り、$N\subset C$ となる近傍 $N$ で $C$ に関して相対コンパクトなものを取る。 $\{\alpha_n(0)=p_n\}$ は全て $N\cap I^+(S)$ に含まれているとしてよい。 $\alpha_n(t_n)\in\partial N$ となる最小の $t_n$ に対して、$e_n=\alpha_n(t_n)$ とおく。 causal曲線の族に対する擬極限における極限点列の作り方から、$e_n\rightarrow e\in J^-(p)$ である。

このとき構成の仕方から $e\in\partial N\subset I(S)$ であるが、以下のように $e\notin I(S)$ を示すことが出来る。 $e\in J^-(p)\subset J^-(S)$ より $J^+(p)\cap S\neq\emptyset$ であるから、もし $e\in I^+(S)$ とすると、$J^+(e)\subset J^+(I^+(S))=I^+(S)$ であるから $S\cap I^+(S)\neq\emptyset$ となり $S$ がachronalであることに矛盾するから、$e\notin I^+(S)$ である。 さらに $e\in J^-(p),\ e\ne p$ かつ $S$ がacausalであるから $e\notin S$ でもある。 またもしある $\alpha_n$ が $I^-(S)$ と交わるなら $\alpha_n$ は $p_n\in I^+(S)\cap N$ から出て $S$ と交わらず $I^-(S)$ と交わるcausal曲線となり $S\cap edg(S)=\emptyset$ であることに矛盾する。 よってどの $\alpha_n$ も $I^-(S)$ と交わらないから、$e\notin I^-(S)$ である。 よって $e\notin I(S)$ であり矛盾を生じる。 $\square$

□

Step2.

　$I(S)=I^+(S)\sqcup S \sqcup I^-(S)$ であるから、$S$ は $I(S)$ の中では閉集合である。 もしこのとき $I^\pm(S)\cap D(S)$ が開集合であることが従うならば、補題(1)と合わせると $I(S)$ の中で $D(S)$ は開集合である。 さらに $I(S)$ は $M$ の中で開集合であるから、$D(S)$ は $M$ でも開集合となる。 従って、次の補題2を示せばよい。

補題 (2)

$S$ が閉集合であるとき、$I^+(S)\cap D(S)$ は開集合である。

Proof.

$p\in D^+(S)-S=I^+(S)\cap D(S)$ が内点ではないと仮定する。 すると補題(1)と同様の議論により、過去向きの延長不可能なcausal曲線の族 $\{\alpha_n\}$ で、$\alpha_n(0)\notin D^+(S),\ \alpha_n(0)\rightarrow p$ となり、かつ全ての $\alpha_n$ が $S$ と交わらないものが存在する。

$S$ が閉であることと補題(1)より、局所有限な凸近傍系 $\mathfrak{R}$ で「各要素（凸近傍）は $int(D(S))$ に含まれないならば $S$ と交わらない」という条件のものが存在する。 $\mathfrak{R}$ に関する $\{\alpha_n\}$ の擬極限曲線を $\lambda$ とする。

$\lambda$ は過去向きの延長不可能な $p$ を通るcausal曲線なので $S$ とただ一点 $\lambda_s$ と交わる。 極限点列 $\{p_k\}$ の中で $p_i>\lambda_s\geq p_{i+1}$ となるものが存在し、$p_i$ から $p_{i+1}$ へ至る $\lambda$ の部分曲線は $C\in\mathfrak{R}$ に含まれる。 さらに $\mathfrak{R}$ の構成方法から $C\subset int(D(S))$ である。

よって $p_i\in C\subset D(S)$ であり、$p_i\in D^-(S)$ だとすると $S$ がacausalであることに矛盾するから $p_i\in D^+(S)$ となり、従って $D^+(S)$ は $p_i$ の近傍である。 よって十分大きい $n$ に対して、$\alpha_n$ は $D^+(S)$ と交わる。 これは $\{\alpha_n\}$ が $S$ と交わらないことに矛盾する。 $\square$

□

□

Cauhcy地平面

achronal集合 $A$ に対して、依存領域 $D(A)$ の“境界”が以下に定義するCauchy horizonである。

定義 32 (Cauchy horizon)

achronal集合 $A\subset M$ に対して、$A$ のfuture Cauchy horizon(未来Cauchy地平面) $H^+(A)$ は $H^+(A):=\overline{D^+(A)}\backslash I^-(D^+(A))$ と定義される。 past Cauchy horizon $H^-(A)$ も同様である。 $H(A):=H^+(A)\cup H^-(A)$ を $A$ のCauchy horizonと呼ぶ。

例 (Cauchy horizonの例)

(1) Minkowski時空 $M$ において直交座標系を $\{t,x,y,z\}$ とするとき、ある $t_0\in\mathbb{R}$ に対して $A=\{(t_0,x,y,z)\in M\}$ はachronalであり、$H(A)=\emptyset$ である。

(2) Minkowski時空 $M$ において直交座標系を $\{t,x,y,z\}$ とするとき、$A=\{(t,x,y,z)\in M;\ -t^2+x^2+y^2+z^2=-1,\ t<0\}$ はachronalであり、$H^+(A)=\{(t,x,y,z)\in M;\ -t^2+x^2+y^2+z^2=0,\ t\le0\},\ H^-(A)=\emptyset$ である。

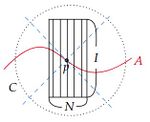
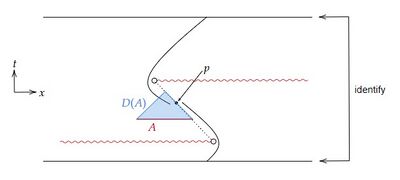
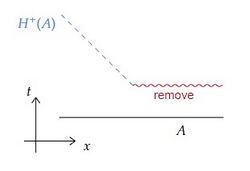
(3) 下図のように2次元Minkowski時空から赤波線を取り除いた時空を考え、$A:=\{(t_0,x);\ {}^\exists t_0\in\mathbb{R}\}$ とすると、$H^+(A)$ は青点線となり、$H^-(A)=\emptyset$ である。

Cauchy地平面はachronalな閉集合 $S$ がCauchy超曲面であることの特徴付けを与えることができる。 以下はこの定理の証明を与える。

依存領域 $D(A)$ はcausal曲線を使って定義されるため、achronalityとの相性があまり良くない。 そこで依存領域の類似の概念として $\tilde D(A)$ を導入する。

定義 33

achronal集合 $A$ に対して、 $$ D_t^+(A):=\{p\in M;\ pを通る任意の過去向きの延長不可能なtimelike曲線がAと交わる\} $$ と定義する。 $D_t^-(A)$ についても過去と未来を入れ替えて同様に定義する。 また $D_t(A):=D_t^+(A)\cup D_t^-(A)$ とする。

$D(A),D_t(A),H(A)$ の関係は次である。

補題 34

achronalな閉集合 $A$ に対して、

(1) $\overline{D(A)}=D_t(A)$

(2) $intD(A)=int D_t(A)$

(3) $\partial D(A)=\partial D_t(A)=H(A)$

となる。

Proof.

(1)の証明

$q\notin \overline{D^+(A)}$ とすると、$ext(D^+(A))$ は開集合だから $r\in I^-(q,ext(D^+(A)))$ があって $r$ を通る延長不可能な過去向きのcausal曲線で $A$ と交わらないものが存在する。 よって補題21より $q$ を通る延長不可能な過去向きのtimelike曲線で $A$ と交わらないものも存在するから、$q\notin D_t(A)$ である。 従って、$D_t(A)\subset\overline{D^+(A)}$ である。

次に $p\in\overline{D^+(A)}-D_t(A)$ とする。 仮定より $p$ を通る延長不可能な過去向きのtimelike曲線 $\alpha$ で $A$ と交わらないものがある。 $p\in\overline{D^+(A)}$ だから $p$ に十分近い $\alpha$ 上の点 $p^-$ に対してある点 $q\in I^+(p^-)\cap D^+(A)$ が存在し、$p^-$ と $q$ をtimelike曲線でつなげれば $q$ を通る延長不可能な過去向きのtimelike曲線で $A$ と交わらないものが得られ、$q\in D^+(A)$ であることに矛盾する。 よって $\overline{D^+(A)}-D_t(A)=\emptyset$ であるから、$\overline{D^+(A)}=D_t(A)$ である。 $\square$

□

(2)の証明

$ intD(A)\subset int D_t(A)$ は明らかなので逆を示す。 $ p\in int \tilde D(A)\subset I^+(A)\cup I^-(A)\cup S$ であるから、(i) $p\in I^-(A)$, (ii) $p\in A$ のときに $p\in int D(A)$ が成り立つことを示せば良い。

(i) $p\in I^-(A)$ のとき

$p\in int D^-(A)$ となることを示す。 $A$ はachronalであるから $p\notin D_t^+(A)$ であるから、$p\in D_t^-(A)$ である。

(ii) $p\in A$ のとき

$\square$

□

(3)の証明

$\square$

□

□

Cauchy地平面によりCauchy超曲面の特徴付けが次である。

命題 35

$S$ をachronalな閉集合とするとき、$ D_t(S)=M\Leftrightarrow D(S)=M\Leftrightarrow H(S)=\emptyset$ が成り立つ。

Proof.

$\square$

□

Globally hyperbolic時空のCauchy超曲面による特徴づけ

Cauchy超曲面が存在するならばGlobally hyperbolicであることは既に示した。 ここではGlobally hyperbolicならばCauchy超曲面が存在することを示す。

証明には次の補題を使う。

補題 36

Globally hyperbolic時空 $(M,g)$ において、$\mu(M)=1$ となるRiemannian測度 $\mu$ に関する体積時間を $t^\pm(p)=\mu(I^\pm(p))$ とする。 このとき連続関数 $$ t(p):=\log\left(-\frac{t^-(p)}{t^+(p)}\right) $$ は任意の延長不可能な未来向きのcausal曲線 $\gamma:(a,b)\rightarrow M$ に対して、 $$ \lim_{s\rightarrow a}t(\gamma(s))=-\infty,\ \lim_{s\rightarrow b}t(\gamma(s))=\infty, $$ を満たす。

Proof.

$\lim_{s\rightarrow a}t^-(\gamma(s))=0,\ \lim_{s\rightarrow b}t^+(\gamma(s))=0$ を示せば良い。 同様なので $\lim_{s\rightarrow a}t^-(\gamma(s))=0$ のみ示す。 $\lim_{s\rightarrow a}t^-(\gamma(s))\ne 0$ と仮定し矛盾を導く。 仮定より、ある $s_0$ に対して、$\mu(\bigcap_{s\le s_0}I^-(\gamma(s)))>0$ であるから、$\bigcap_{s\le s_0}I^-(\gamma(s))\cap K\ne\emptyset$ となるコンパクト集合 $K$ が存在する（詳細な議論は2を参照されたい）。 $s_i\rightarrow a$ となる列 $\{s_i\}_{i\geq0}$ を取り、$p_i=\gamma(s_i)$ とする。 さらに点列 $r_i\in I^-(\gamma(p_i))\cap K$ を任意に取る。 $r_i\rightarrow r\in K$ となるから、$p<<r$ となる $p$ に対して、$p<<p_i<p_0$ となる。 よって $\gamma((a,s_0])\subset J(p,p_0)$ となる。 $J(p,p_0)$ はコンパクトであり、strongly causal時空では延長不可能なcausal曲線がコンパクト集合に含まれることはありえないという事実に矛盾する。

□

命題 37

Globally hyperbolicならばCauchy超曲面が存在する。

Proof.

globally hyperbolic時空はcausally continuous時空であるから体積時間 $t^\pm$ はtime functionとなる。 よって $t$ もtime functionである。 また $t^{-1}(0)$ はachronal集合である。 任意の延長不可能なcausal曲線 $\gamma$ に対して、適当にパラメータを取ると上の命題より $\gamma(c)\in t^{-1}(0)$ となる $c\in\mathbb{R}$ がただ一つ存在する。 よって $t^{-1}(0)$ はCauchy超曲面である。

□

以上により次の結果が得られた。

定理 38 (globally hyperbolic時空のCauchy超曲面による特徴づけ)

時空 $(M,g)$ がglobally hyperbolicであることとCauchy超曲面 $S$ を持つことは同値である。 さらにこのとき、Cauchy time functionが存在し、また任意のCauchy超曲面は $S$ と同相であり、$M$ は $S\times\mathbb{R}$ と同相である。

Cauchy超曲面の滑らかさと大域的直交分解

Cauchy超曲面やCauchy time functionは滑らかかという問題意識が生じるのは当然である。 これらが滑らかであるという仮定は議論の有用な単純化と応用性を持つため多くの研究で採用されてきたにも関わらず、長い間その証明は知られていなかった。 この事情からこれらはCauchy超曲面の滑らかさに関する“民間問題”(folk problems)と呼ばれていた。 これらの問題は2003～2006年にかけてBernalとSánchezにより肯定的に証明された3,4,5。

滑らかでかつ空間的なCauchy超曲面が存在すれば、その時空は時間×空間という多様体に位相同型なだけでなく微分同相となる。 さらに、Cauchy temporal function $T$ が存在すれば、時空の計量は $\beta\in C^\infty(M)$ と リーマン計量の族 $h_T$ により、$g=-\beta^2dT^2+h$ と表される。 $h_T$ は $T$ の各レベル集合へ誘導される誘導計量である。 すなわち、このとき時空が時間と空間に大域的に直交分解される。 また与えられたCauchy $S$ 上での初期値問題を定式化するためには、Sをレベル集合に持つCauchy temporal function $T$ が存在するかどうかも重要である。 量子化の観点からはどのような条件の空間的部分多様体がCauchy超曲面に拡張できるかという問題も有用である。 これらに対する結果をまとめた定理が以下である。

命題 39 (Cauchy超曲面の滑らかさ)

時空 $(M,g)$ がGlobally hyerbolic時空であることと、滑らかな空間的Cauchy超曲面 $S$ が存在することは同値である。 さらにこのとき、Cauchy temporal function $T$ が存在し、$M$ は $\mathbb{R}\times S$ と微分同相であり、計量は $$ \begin{aligned} g=-\beta dT^2+g_{T} \end{aligned} $$ と表される。 ここで $\beta$ は正値の $M$ 上の滑らかな関数であり、$g_{T}$ は $T$ の各レベル集合 $S_T$ 上のリーマン計量である。

命題 40 (Cauchy超曲面に対する滑らかなCauchy functionの存在)

時空 $(M,g)$ がGlobally hyperbolic時空であるとき、与えられた(topological) Cauchy超曲面 $S$ に対して、滑らかなCauchy function $\tau$ が存在し、$\tau^{-1}(0)=S$ となる。 さらに、$S$ がacausalなら $\tau$ はCauchy time functionとなり、$S$ が空間的ならば $\tau$ を必要なら修正することで Cauchy temporal function $T$ で $T^{-1}(0)=S$ となるものを得ることが出来る。

命題 41 (Cauchy超曲面への延長可能性)

Globally hyperbolic時空 $(M,g)$ のコンパクトachronal部分集合 $A$ はCauchy超曲面に拡張することができる。 さらに $A$ がacausalかつ境界を持つ滑らかな空間的超曲面であるなら空間的なCauchy超曲面に拡張することができる。

出典

• 1 Barrett O'neill.. "Semi-Riemannian geometry with applications to relativity.". Academic press (1983): 419.
• 2 Sánchez, Miguel.. (2004) "Causal hierarchy of spacetimes, temporal functions and smoothness of Geroch's splitting. A revision.". arXiv preprint gr-qc/0411143 (2004) .
• 3 Bernal.A.N. and Sánchez.M.. (2005) "On smooth Cauchy hypersurfaces and Geroch's splitting theorem.". Commun. Math. Phys. 243, 461–470 .

• 4 Bernal.A.N. and Sánchez.M.. (2005) "Smoothness of time functions and the metric splitting of globally hyperbolic spacetimes.". Commun. Math. Phys. 257, 43–50 .
• 5 Bernal.A.N. and Sánchez.M.. (2006) "Further results on the smoothability of Cauchy hypersurfaces and Cauchy time functions.". Lett. Math. Phys. 77, 183–197 .