因果階層
因果階層(causal hierarchy)とは、Lorentz多様体の特徴的な因果構造についての性質の包含関係の事である。 その包含関係は、Non-totally vicious $\supset$ chronological $\supset$ causal $\supset$ distinguishing $\supset$ strong causal $\supset$ stably causal $\supset$ causally continuous $\supset$ causally simple $\supset$ globally hyperbolic である。 この記事では、それぞれの定義と例、またいくらかの顕著な定理について述べる。 この分野の国内での広く知れ渡った和訳の文化はおそらく確立していないため固有名称については英単語のままで解説する。1
因果構造に関するいくつかの事項
因果階層のそれぞれのクラスを定義するために種々の因果構造に関する概念や事実を必要とする。 ここで述べる事項は因果階層の各クラスと密接に関係した概念であるものの定義や基本的な性質自体は因果階層と独立に与えられるため、因果階層の解説の前にここでまとめる。
基本的な概念と用語
時間的向き付け可能なLorentz多様体 $(M,g)$ は"時空" (spacetime) と呼ばれる。 区分的 $C^1$ 級の曲線 $\gamma:I\rightarrow M$ が未来向きtimelike曲線であるとは、接ベクトルが常に未来向きのtimelikeベクトルとなることである。 区分的 $C^1$ 級の曲線 $\gamma:I\rightarrow M$ が未来向きcausal曲線であるとは、接ベクトル $\dot{\gamma}$ が常に未来向きで、かつ $||\dot{\gamma}||^2\geq0$ となることである。
時間的向き
Lorentz多様体 $(M,g)$ が時間的向き付け可能とは、Mの開被覆 $\{O_i\}$ と各 $\{O_i\}$ 上の時間的ベクトル場 $X_i$ の組 $\{(O_i,X_i)\}$で、$O_i\cap O_j(\ne\emptyset)$ 上で $g(X_i,X_j)<0$ となるものが存在するときをいう。 このとき 各点 $p\in M$ に対して、$p\in O_i$ となる $i$ に対して、$X_i(p)$ が $p$ における未来向きを定める。 また時間的向き付け可能なLorentz多様体を時空と呼ぶ。 時空 $M$ が時間的向き付け可能であるための必要十分条件は明らかに次である。
命題 1 (時間的向き付け可能であることの必要十分条件)
Lorentz多様体 $(M,g)$ が時間的向き付け可能であることの必要十分条件は、$M$ 全体で定義された時間的ベクトル場が存在することである。
Proof.
Lorentz多様体 $(M,g)$ が時間的向き付け可能であるとすると、上の定義の開被覆と時間的ベクトル場の組 $\{(O_i,X_i)\}$ を取り、$\{O_i\}$ に関する1の分割 $\{\rho_i\}$ をとり、$X=\sum_i\rho_iX_i$ とすると、$X$ は $M$ 全体で定義された時間的ベクトル場である。 逆に、$M$ 全体で定義された時間的ベクトル場 $X$ があるとする。 $M$ 上の任意のリーマン計量 $g_R$ をとり、$g(Y,Z):=g_R(Y,Z)-2||X||_R^{-2}g_R(X,Y)g_R(X,Z)$ と置くと $g(X,X)=-||X||_R^2<0$ であり、$g$ はLorentz計量である。 さらに $\{O_i,X|_{O_i}\}$ は上の定義の要件を明らかに満たすから $g$ は時間的向き付け可能である。
□Lorentz多様体 $(M,g)$ が時間的向き付け可能でなくても次の処方で時間的向き付け可能なLorentz多様体を得ることができる。$\tilde{M}:=\{(p,C),\ p\in M,\ C は T_pM の2つの{\rm causal\ cone}のどちらか\}$ とする。このとき $\pi:\tilde{M}\ni(p,C)\mapsto p\in M$ は被覆写像であり、$\tilde{M}$ は $M$ の二重被覆多様体である。さらに $\tilde{g}:=\pi^\ast g$ として $\tilde{M}$ に計量を定める。このとき、$\tilde{M}$ が連結でない、すなわち2つの連結成分を持つなら $M$ 自体が時間的向き付け可能である。したがって $M$ が時間的向き付け可能でないなら $\tilde{M}$ は連結である。$\tilde{M}$ が連結ならその各点にはcausal coneのうちの一つが連続的に割り当てられているので $\tilde{M}$ は時間的向き付け可能である。
さらに次の定理が成り立つ。
定理 2
滑らかな多様体 $M$ に対して以下は同値である。
(1) $M$ 上にLorentz計量が存在する。
(2) $M$ 上に時間的向き付け可能なLorentz計量が存在する。
(3) $M$ 上に至る所0にならない大域的なベクトル場 $X$ が存在する。
(4) $M$ はコンパクトでないか、またはEuler標数が0である。
Proof.
$(3)\Leftrightarrow(4)$ 微分トポロジーからの帰結である。
$(2)\Rightarrow(3)$ 上の命題から従う。
$(3)\Rightarrow(2)$ $M$ 上に任意にリーマン計量 $g_R$ を定めるとき、$g_L:=g_R-\frac{2}{g_R(X,X)}{}^\flat X\otimes{}^\flat X$ は向き付け可能なLorentz計量を定める。
$(2)\Rightarrow(1)$ 自明である。
$(1)\Rightarrow(2)$ $(M,g)$ の時間的向き付け可能な二重被覆多様体 $(\tilde{M},\tilde{g})$ は(4)を満たす。したがって $M$ も(4)を満たす。
□時間的未来(過去)、因果的未来(過去)
$p\in M$ に対して、未来向きtimelike曲線 $\gamma:[0,1]\rightarrow M$ で $\gamma(0)=1,\gamma(1)=q$ となるものが存在するとき、$p<<q$ と書く。 $$ \begin{align} I^+(p):=\{q\in M;\ p<<q\} \end{align} $$ を $p$ の時間的未来 (timelike future) と呼ぶ。 また未来向きcausal曲線 $\gamma:[0,1]\rightarrow M$ で $\gamma(0)=p,\gamma(1)=q$ となるものが存在するとき、$p\le q$ と書く。 $$ \begin{align} J^+(p):=\{q\in M;\ p\le q\} \end{align} $$ を $p$ の因果的未来 (causal future) と呼ぶ。
$I^\pm,J^\pm$ は $M$ から $M$ の冪集合 $\mathcal{P}(M)$ への写像とみなすことができる。
定義 3 (内側連続、外側連続の定義)
$I^\pm:M\rightarrow\mathcal{P}(M)$ が
(1) 内側連続 (inner continuous)であるとは、任意の $p\in M$ と任意のコンパクト集合 $K\subset I^\pm(p)$ に対して、$p$ の適当な近傍 $U$ が存在し、任意の $q\in U$ に対して、$K\subset I^\pm(q)$ となるときを言う。
(2) 外側連続 (outer continuous)であるとは、任意の $p\in M$ と任意のコンパクト集合 $K\subset M\backslash \overline{I^\pm(p)}$ に対して、$p$ の適当な近傍 $U$ が存在し、任意の $q\in U$ に対して、$K\subset M\backslash \overline{I^\pm(q)}$ となるときを言う。
命題 4 ($I^\pm$ の内側連続性)
$I^\pm$ は常に内側連続である。
Proof.
任意の $p\in M$ と任意のコンパクト集合 $K\subset M\backslash \overline{I^\pm(p)}$ に対して、$\{I^\pm(q);\ a\in I^\pm(p)\}$ は $K$ の開被覆である。 従って、有限個の $q_i\in I^\pm(p)$ を選んで、 $K\subset\bigcup_{q_i}I^\pm(q_i)$ と出来る。 このとき、$\bigcap_{q_i}I^\mp(q_i)$ は $p$ の近傍であり、望みの条件を満たす。
□achronal set、acausal set
部分集合 $A\subset M$ がachronal (resp. acausal)とは、$A$ の任意の2点がtimelike曲線 (resp. causal曲線) で結ばれないことである。
$I^\pm,J^\pm$ に関する基本的な事項
ここでは $I^\pm$ と $J^\pm$ のそれぞれの性質とこれらの関係性についていくつかの事項をまとめる。
命題 5
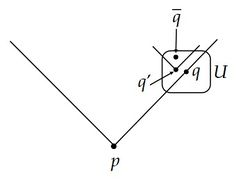
$<<$ はopenである。すなわち、$p<<q$ であるとき、適当な $p$ の近傍 $U$ と適当な $q$ の近傍 $V$ があり、任意の $p'\in U,\ q'\in V$ に対して、$p'<<q'$ が成り立つ。
Proof.
$p,q$ を結ぶ時間的曲線を $\alpha$ とし、$p,q$ の凸近傍をそれぞれ $C,D$ とする。 $C\cap\alpha$ の点で $p$ の未来にあるものを一つ選び $p^+$ とし、$D\cap\alpha$ の点で $q$ の過去にあるものを一つ選び $q^-$ とする。 $U:=C\cap I^-(p^+),\ V:=D\cap I^+(q^-)$ とすると、作り方から $U,V$ は望みの性質を持つ。
□命題 6
$(1)\ \overline{I^\pm}(p)=\overline{J^\pm}(p),\ (2)\ {\rm int}J^\pm(p)=I^\pm(p),\ (3)\ \partial J^\pm(p)=\partial I^\pm(p)$
Proof.
$(1)\ \overline{I^\pm}(p)=\overline{J^\pm}(q)$ の証明
$I^+(p)\subset J^+(p)$ より $\overline{I^+}(p)\subset\overline{J^+}(p)$ である。 逆の包含関係を示す。 $q\in \overline{J^+}(p)$ とする。 $q$ の任意に小さい近傍を $U$ とすると、$q\in \overline{J^+}(p)$ であるから、$U$ は $q'\in J^+(p)$ となる点 $q'$ を含む。 任意の $\bar{q} \in U\cap I^+(q')$ に対して、$\bar{q}\in I^+(J^+(p))=I^+(p)$ であり、$U$ は任意に小さく取れるから $q$ は $I^+(p)$ の点列の集積点となり得る。 よって $\overline{I^+}\supset\overline{J^+}$ である。
$(2)\ {\rm int}J^\pm(p)=I^\pm(p)$ の証明
$I^+(p)$ は開集合であり、$I^+(p)\subset J^+(p)$ であるから、$I^+(p)\subset {\rm int}J^+(p)$ である。 逆の包含関係を示す。 $q\in {\rm int}J^+(p)$ とすると、$q$ の近傍 $U$ で $q\in U\subset {\rm int}J^+(p)$ となるものが存在する。 任意の $q'\in U\cap I^-(q)$ に対して、$q'\in J^+(p)$ であるから、$q\in I^+(q')\subset I^+(J^+(p))=I^+(p)$ である。
$(3)\ \partial J^\pm(p)=\partial I^\pm(p)$ の証明
(1),(2)と $\partial S=\overline{S}\backslash{\rm int}S$ より明らかである。
□命題 7
$J^\pm(I^\pm(p))=I^\pm(J^\pm(p))=I^\pm(p)$
Proof.
曲線の変分論による。(途中)
□時間関数
時空の因果構造に関する興味の一つとして、その時空に“大域的な時間”を定義できるかという問題である。 “大域的な時間”とは因果的に隔たった事象間の因果的な隔たり具合を測る時空全体で定義された尺度を提供するものであると考えられるから次のように定義をする。
定義 8 (時間関数の定義)
時空 $(M,g)$ 上のスカラー関数 $t:M\rightarrow\mathbb{R}$ は、
(1) 任意の未来向きcausal曲線に沿って狭義単調増加となるとき、一般化time functionという。
(2) 一般化time functionで連続であるとき、time functionという。
(3) 滑らかでかつ $\nabla t$ が過去向きtimelikeベクトル場であるとき、temporal functionという。
(time functionとtemporal functionを訳し分けにくいので英単語のままにする)
上の3種類の時間関数の存在は(以下で登場する)いくつかの時空の因果構造の特徴づけに有効である。
time separation(時間間隔)
時空の $p<q$ となる2点が時間的にどれぐらい隔たっているかを測ることが出来る。 これが次のtime separation(時間間隔)である。
定義 9 (time separationの定義)
時空 $(M,g)$ に対して、time separation(時間間隔)$\tau:M\times M\rightarrow\mathbb{R}$ を $$ \tau(p,q):=\sup\{L(\gamma);\ \gamma:[0,1]\rightarrow Mは\gamma(0)=p,\gamma(1)=qとなる未来向きcausal曲線\} $$ と定義する。 ただし、$p,q$ を結ぶ未来向きのcausal曲線が存在しないときは、$\tau(p,q)=0$ と定める。
time separationの基本的な性質は次である。
命題 10 (time separationの基本的性質)
(1) $\tau(p,q)>0\ \Leftrightarrow\ p<<q$
(2) $p\le q\le r$ のとき、$\tau(p,r)\geq\tau(p,q)+\tau(q,r)$ (逆三角不等式)
Proof.
(1) $\tau(p,q)>0$ とすると、$p,q$ を結ぶ未来向きのcausal曲線 $\alpha$ で $L(\alpha)>0$ となるものが存在する。 $\alpha$ はヌル測地線ではないから端点を固定した変分によりtimelike曲線に変形できる。 従って、$p<<q$ である。 逆は明らかである。
(2) $p,q$ を結ぶcausal曲線 $\alpha$ と $q,r$ を結ぶcausal曲線を $\beta$ を適切に選べば、任意の小さい $\delta$ に対して $L(\alpha)\geq\tau(p,q)-\delta/2,\ L(\beta)\geq\tau(q,r)-\delta/2$ となるようにできる。 よって $\tau(p,r)\geq L(\alpha\cup\beta)\geq\tau(p,q)+\tau(q,r)-\delta$ となり、不等式が従う。
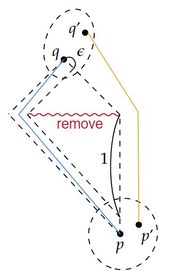
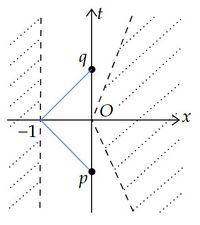
□一般にtime separationは連続関数ではない。
この例では $p,q$ を結ぶtimelike曲線(青線)の長さは、$\epsilon$ を小さく取れば、いくらでも0に近くなるから $\tau(p,q)$ はいくらでも小さくできる。 しかし $p,q$ それぞれの任意の近傍から適当に $p',q'$ を取ると $p',q'$ を結ぶtimelike曲線(黄線)の長さが1に近いものがある。 従って $p,q$ の近くに制限しても $\tau$ が大きくなる範囲が一定値より小さくなるようにすることはできない。 この例から $\tau$ は上半連続ではないことが分かる。
半連続の定義
$X$ を位相空間とするとき、写像 $f:X\rightarrow\mathbb{R}$ が点 $p\in X$ において連続であるとは、任意の $\varepsilon>0$ に対して、ある $p$ の近傍 $U$ があって、任意の点列 $\{p_n\}\in U,\ p_n\rightarrow p$ が $-\varepsilon<f(p_n)-f(p)<\varepsilon$ を満たすことである。 $f$ が下半連続であるとは最後の式が $-\varepsilon<f(p_n)-f(p)$ となることであり、同様に上半連続であるとは $f(p_n)-f(p)<\varepsilon$ となることである。 下半連続(上半連続)とは任意に少しだけ小さくなる(大きくなる)近傍があるということである。
□命題 11 (time separationの下半連続性)
任意の時空においてtime separationは下半連続である。
Proof.
$\tau(p,q)=0$ のときは定義より $(p,q)$ において下半連続である。 $0<\tau(p,q)<\infty$ とする。 $p,q$ を結ぶtimelike曲線 $\alpha$ で $L(\alpha)>\tau(p,q)-\delta$ となるものが存在する($\delta$ は任意の小さい正数)。 $\alpha$ 上の $p,q$ に十分近い点をそれぞれ $p_0,q_0,\ (p<<p_0,q_0<<q)$ とする(適当な凸近傍内に選べばよい)。 $p,p_0$ を結ぶ測地線を $\overline{pp_0}$、$q_0,q$ を結ぶ測地線を $\overline{q_0q}$ とする。 $p$ の近傍 $V_p$ で任意の $p_1\in V_p$ に対して、$L(\overline{p_1p_0})\geq L(\overline{pp_0})-\delta$ が成り立つものが取れる(凸近傍内ではtimelike曲線の長さは端点に関して連続であり、$p_1=p$ に対してこの不等式は成り立つから)。 同様に、$q$ の近傍 $V_q$ で任意の $q_1\in V_q$ に対して、$L(\overline{q_0q_1})\geq L(\overline{q_0q})-\delta$ が成り立つものが取れる。 よって任意の $p_1\in V_p,\ q_1\in V_q$ に対して、 $$ \begin{aligned} \tau(p_1,q_1)&\geq L(\overline{p_1p_0})+L(\alpha(p_0\rightarrow q_0))+L(\overline{q_0q_1}) \geq L(\overline{pp_0})+L(\alpha(p_0\rightarrow q_0))+L(\overline{q_0q})-2\delta\\ &\geq L(\alpha(p\rightarrow p_0)+L(\alpha(p_0\rightarrow q_0))+L(\alpha(q_0\rightarrow q))-2\delta\\ &\geq L(\alpha)-2\delta \geq \tau(p,q)-3\delta \end{aligned} $$ となり、下半連続であることが分かる。
□体積関数
時空上に時空全体での積分が有限となるような測度を導入して、その測度に関する時空の部分領域の体積を考えることができる。 これを利用すると特定の時空では時間関数を構成することができる。
定義 12 (体積関数の定義)
時空 $(M,g)$ において、Borel測度 $\mu$ で $\mu(M)<\infty$ となるもの任意に一つ取り、固定する。 このとき、$\mu$ に付随する過去体積関数(past volume function) $t^-:M\rightarrow\mathbb{R}_{\geq0}$、未来体積関数(future volume function) $t^+:M\rightarrow\mathbb{R}_{\le0}$ を次で定義する。 $$ \begin{align} t^-(p)&:=\mu(I^-(p)),\\ t^+(p)&:=-\mu(I^+(p)) \end{align} $$
上の定義で用いた時空 $(M,g)$ 上のBorel測度 $\mu$ は例えば次のようにして構成できる。 $g$ から定まるリーマン測度を $\omega$ とし、$M$ の開被覆 $\{U_i\}_{i\in\mathbb{N}}$ で $\mu(U_i)<1$ となるものを取る。 開被覆 $\{U_i\}_{i\in\mathbb{N}}$ に付随する1の分割を $\{\rho_i\}$ とする。 このとき、$\mu:=\sum_i2^{-i}\rho_i\omega$ は望みの性質を満たす。
命題 13 (体積関数の半連続性)
$t^-$ (resp. $t^+$) は下 (resp. 上) 半連続である。
Proof.
$p\in M$ に対して、$p$ に収束する点列 $\{p_i\},\ p_i\rightarrow p (i\rightarrow\infty)$ を任意に取る。任意の $\epsilon>0$ に対して、ある $N\in\mathbb{N}$ があり、$n>N$ ならば、$t^-(p_n)>t^-(p)-\epsilon,\ t^+(p_n)<t^+(p)+\epsilon$ であることを示せばよい。 コンパクト集合 $K\subset I^-(p)$ で $\mu(K)>I^-(p)-\epsilon$ となるものが存在し、さらに $I^-$ の内側連続性より、ある $N\in\mathbb{N}$ があり、$n>N$ ならば、$K\subset I^-(p_n)$ である。 よって、$t^-(p_n)>\mu(K)>I^-(p)-\epsilon$ となる。 同様に、コンパクト集合 $K\subset I^+(p)$ で $\mu(K)>-I^+(p)-\epsilon$ となるものが存在し、さらに $I^+$ の内側連続性より、ある $N\in\mathbb{N}$ があり、$n>N$ ならば、$K\subset I^+(p_n)$ である。 よって、$t^+(p_n)>\mu(K)<I^+(p)+\epsilon$ となる。
□$p<<q$ ならば、$I^-(p)\subset I^-(q)$ であるから、$t^-(p)\le t^-(q)$ である。従って、$t^-$ は任意のtimelike曲線に沿って広義単調増加である。 $t^+$ も同様の理由から任意のtimelike曲線に沿って広義単調増加である。 しかし一般には狭義単調増加になるとは限らない。 また連続であることも一般には成り立たない。 従って、一般には $t^\pm$ は一般化time functionですらない。
因果構造の連続性
常に $t^-$ は下半連続、$t^+$ は上半連続、$I^\pm$ は内側連続であるが、$t^\pm$ は連続とは限らないし、$I^\pm$ も外側連続とは限らいない。 後者も成り立つなら、因果構造自体がある意味で連続であると言える。 ここでは因果構造が連続であるということの意味をはっきりさせ、いつくかの特徴づけを与える。
命題 14 (体積関数と $I^\pm$ の連続性)
$t^\pm$ が連続であることと $I^\pm$ が外側連続であることは同値である。
Proof.
$I^-$ が外側連続であるとする。 $t^-$ を測度 $\mu$ に関する過去体積関するとする。 任意の点 $p\in M$ に対して、$K\subset M\backslash \overline{I^-(p)}$ で $\mu(M\backslash \overline{I^-(p)})-\varepsilon<\mu(K)$ となるコンパクト集合 $K$ を取ると、外側連続性より $p$ の近傍 $U$ があり、点列 $\{p_n\}\in U,\ p_n\rightarrow p$ に対して、$K\subset M\backslash \overline{I^-(p_n)}$ となる。 よって $t^-(p_n)<\mu(M)-\mu(K)<t^-(p)+\varepsilon$ であるから上半連続である。 $t^-$ は常に下半連続であるから連続である。
逆に $t^-$ が連続、従って上半連続であるとする。
□$I^\pm$ が外側連続であるとき、$I^\pm$ を $M$ から $M$ の冪集合への写像と見ても連続である。 従ってこのとき、単に $I^\pm$ が連続であるということがある。 $t^\pm$ が連続であったとしてもtime functionになるとは限らない。
因果構造の連続性に関してもう一つ同値な特徴づけがある。 それが以下の反射律である。
定義 15 (反射律)
時空 $(M,g)$ が点 $q\in M$ において過去反射的(past reflecting) (resp. 未来反射的(future reflecting)) であるとは、次の同値な3つの条件を満たすときを言う。
(1) $I^+(p)\supset I^+(q)\ \Rightarrow\ I^-(p)\subset I^-(q)$ (resp. $I^-(p)\supset I^-(q)\ \Rightarrow\ I^+(p)\subset I^+(q)$)
(2) $q\in \overline{I^+(p)}\ \Rightarrow\ p\in \overline{I^-(q)}$ (resp. $q\in \overline{I^-(p)}\ \Rightarrow\ p\in \overline{I^+(q)}$)
(3) $q\in \partial I^+(p)\ \Rightarrow\ p\in \partial I^-(q)$ (resp. $q\in \partial I^-(p)\ \Rightarrow\ p\in \partial I^+(q)$)
さらに任意の点が過去反射的 (resp. 未来反射的) であるとき、時空 $(M,g)$ は過去反射的 (resp. 未来反射的) であるという。 過去反射的かつ未来反射的であるとき、時空 $(M,g)$ は反射的であるという。
上の3つの条件が同値であることの証明
$(1)\Leftrightarrow(2)$
$I^+(q)\subset I^+(p)\Leftrightarrow q\in\overline{I^+(p)}$ と $I^-(p)\subset I^-(q)\Leftrightarrow p\in\overline{I^-(q)}$ を示せばよい。 $I^+(q)\subset I^+(p)$ とする。 点列 $\{q_n\}\in I^+(q),\ q_n\rightarrow q$ を考えると、$q\in\overline{I^+(p)}$ である。 逆に、$q\in\overline{I^+(p)}=\overline{J^+(p)}$ とする。 $q'\in I^+(q)$ に対して $q,q'$ を結ぶ時間的曲線を $\alpha$とする。 $q$ の小さい近傍を $U$ とし、$\bar{q}\in\alpha\cap U\cap I^+(q)$ を任意に選ぶ。 点列 $\{q_n\}\in I^-(\bar{q})\cap U$ で $q_n\rightarrow q$ かつ $q_n\in I^+(p)$ となるものが存在する($q\in \overline{I^+(p)}$ より)。 このとき $p<<q_n<<\bar{q}<<q'$ であるから $I^+(q)\subset I^+(p)$ である。 よって $I^+(q)\subset I^+(p)\Leftrightarrow q\in\overline{I^+(p)}$ となる。 $I^-(p)\subset I^-(q)\Leftrightarrow p\in\overline{I^-(q)}$ も同様である。
$(2)\Rightarrow(3)$
$q\in \partial I^+(p)$ ならば、$q\in \overline{I^+(p)}$ かつ $q\notin I^+(p)$ である。 (3)を仮定しているから、$p\in\overline{I^-(q)}$ かつ $p\notin I^-(q)$ となり $p\in\partial I^-(q)$ である。
$(3)\Rightarrow(2)$
$q\in\overline{I^+(p)}$ ならば、$q\in\partial I^+(p)$ または $q\in I^+(p)$ である。 (2)を仮定しているから、$p\in\partial I^-(q)$ または $p\in I^-(q)$ となり $p\in\overline{I^-(p)}$ である。
□反射律に関して次が成り立つ。
命題 16 ($I^\pm$ の連続性と反射律との同値性)
時空 $(M,g)$ において、$I^-$ (resp. $I^+$) が(外側)連続であることと、過去反射的 (resp. 未来反射的) であることは同値である。
Proof.
$I^-$ が外側連続であるとする。 特に $q\in M$ において $I^-$ は外側連続であるとする。 $q\in \overline{I^+(p)}$ かつ $p\notin \overline{I^-(q)}$ となる $p\in M$ が存在すると仮定して矛盾を導く。 $p\notin \overline{I^-(q)}$ と $I^-$ の外側連続性により、$q$ の適当な近傍 $V$ があり、任意の $q'\in V$ に対して、$p\notin \overline{I^-(q')}$ とできる。 しかし $q\in \overline{I^+(p)}$ であるから、$q'\in V$ で $p\in I^-(q')$ となるものが存在して矛盾する。
逆に、過去反射的であるとする。 $I^-$ が外側連続でないとして矛盾を導く。 $I^-$ が外側連続でないから、コンパクト集合 $K$ と $p\in M$ で $K\cap \overline{I^-(p)}=\emptyset$ かつ 点列 ${p_n}\rightarrow p$ で $K\cap\overline{I^-}(p_n)\neq\emptyset$ となるものが存在するようなものがある。 点列 $r_n\in K\cap\overline{I^-}(p_n)$ を任意に選び、必要なら部分列を取ることで $r_n\rightarrow r\in K$ とする。 任意の $s \in I^-(r)$ に対して、$n$ が十分大きいとき $p_n\in I^+(s)$ であるから、$p\in\overline{I^+(s)}$ である。 過去反射律より $s\in \overline{I^-(p)}$ であり、従って $I^-(r)\subset\overline{I^-(p)}$ である。 よって $r\in \overline{I^-(r)}\subset\overline{I^-(p)}$ であるが、$r\in K$ であるから、$K\cap \overline{I^-(p)}=\emptyset$ に矛盾する。
□この反射律による特徴付けはしばしば有効である。
曲線の延長可能性、不可能性
ある曲線をそれ以上伸ばすことが出来るかどうかはしばしば重要なことである。 例えば有限な長さの曲線がもしそれ以上伸ばせないとすれば、その曲線の“端”には何らかの時空特異点が存在していることになる。 時空特異点は数学的にも物理的にも興味ある対象である。 ここでは曲線の延長可能性、不可能性を正確に定義する。
定義 17
$\alpha:[0,b)\rightarrow M,\ b\le\infty$ を区分的 $C^1$ 級未来向き因果的曲線とする。 任意の点列 $\{u_i\}\in[0,b),\ u_i\rightarrow b$ に対して、$\alpha(u_i)\rightarrow p\in M$ となる $p\in M$ が存在するとき、$p$ を未来端点(future end point)といい、曲線 $\alpha$ は未来延長可能(future extendible)であるという。 過去端点と過去延長可能も同様に定義する。 また $\alpha:[0,b]\rightarrow M$ は自明な端点 $\alpha(b)$ を持つとし延長可能と定義する。 延長可能でないときは、延長不可能(inextendible)であるという。
直観的に言うと延長可能な曲線は"伸ばす"ことができる。 区分的 $C^1$ 級の未来向き因果的曲線 $\alpha:[0,b)\rightarrow M$ が延長可能であるとする。$\lim_{s\rightarrow p}\alpha(s)=p$ に対して、未来向き因果的ベクトル $v\in T_pM$ を任意に選び、初期位置が $p$ で初期方向が $v$ である区分的 $C^1$ 級の未来向き因果的曲線を $\beta:[0,c)\rightarrow M,\ \beta(0)=p$ とすると、$\tilde{\alpha}:=\alpha\cup\beta$ は必要なら適当にパラメータを取り直すことで、区分的 $C^1$ 級の未来向き因果的曲線となる。 $\tilde{\alpha}$ は $\alpha$ の未来向きの延長となる。
擬極限曲線
因果構造の考察においてcausal曲線の族を考えることは有用である。 causal曲線の列が適当な意味においてcausal曲線に収束する場合は特に特に便利である。
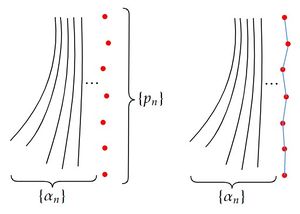
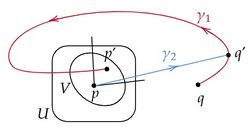
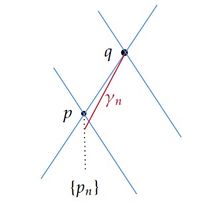
区分的滑らかなcausal曲線の列がある場合、適当な意味でその極限を考えたい。 このとき、その極限も区分的滑らかな曲線として存在すれば便利である。 このような議論を可能にする道具として極限点列(limit sequence)と擬極限曲線(quasi limit curve)である。 下図を使って感覚的に述べると、極限点列はあるcausal曲線の列 $\{\alpha_n\}$ の”極限”を隣接する2点が十分近い点列で近似したもの(赤点)であり、その点達を測地線で結んでできる区分的滑らかなcausal曲線が擬極限曲線である(青線)。
以下詳細に構成を述べる。 まず擬極限曲線が存在するために考える曲線列を次の2つの条件を満たすものに制限して考える。 1つ目は曲線列のそれぞれの曲線の初期位置が収束することであり、2つ目は曲線列が一点に収束しないことである。 すなわち曲線列 $\{\alpha_n\}:[0,b_n)\rightarrow M$ に対して、2つの条件
(i) $\lim_n\alpha_n(0)=p\in M$
(ii) $p$ のある近傍 $V$ が存在し、$\alpha_m([0,b_m))\subset V$ となる $m$ は有限個である
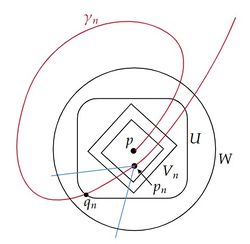
を考える。 (下図は一点に収束する曲線列の例)
次にこの条件を満たす曲線列に対して、極限点列を構成する。 時空 $(M,g)$ の凸近傍による被覆(凸被覆,convex covering)を任意に一つ取りこれを $\mathfrak{R}$ とする。 $\mathfrak{R}$ の局所有限な細分 $\mathfrak{R}'$ を一つ取る(時空はパラコンパクトであるからこれは常に可能である)。 さらに、任意の $C'\in\mathfrak{R}'$ に対して、ある $C\in\mathfrak{R}$ があり、$C'\subset C$ かつ $C'$ は $C$ に関して相対コンパクトであると仮定してよい。
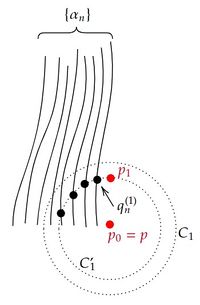
初めに $p_0=p\in C_1'\in\mathfrak{R}'$ として、$q_n^{(1)}:=\alpha_n\cap\partial C_1'$ とする($\alpha_k\cap\partial C_1'=\emptyset$ となる $k$ は有限個なのでそれは除く)。 $\partial C_1'$ はコンパクトなので必要なら部分列を取れば、$q_n^{(1)}\rightarrow p_1\in\partial C_1'$ となる。 またこのとき、$p_0,p_1\in \overline{C_1'}$ であり、ある $C_1\in\mathfrak{R}$ があり、$C_1'\subset C_1$ である。 $C_1$ は凸近傍であり、$\alpha_n(0)\le q_n^{(1)}$ であるから、$p_0\le p_1,\ p_0,p_1\in C_1$ である。 (下図参照)
次に $k\geq1$ に対して $p_k\in C_{k+1}'\in\mathfrak{R}'$ とする。 ただし、このとき
$p_k$ を含む $\mathfrak{R}'$ の元は有限個であり、その有限個の中からこれまでに選ばれた回数が最小のものを選ぶ。$\cdots(\ast)$
このとき次の2つの場合があり得る。
(i) $C'_{k+1}$ から出ていく $\alpha_m$ が有限個の場合
$q^{(k+1)}_n=\alpha_n\cap\partial C'_{k+1}$ とおくと($\partial C'_{k+1}$ と交わらない有限個は除く)、$q^{(k+1)}_n\rightarrow p_{k+1}\in\partial C'_{k+1}$ となる。 特にこのとき、$p_k\le p_{k+1}$ である。
(ii) $C'_{k+1}$ から出ていく $\alpha_m$ が無限個の場合
有限個を除いて $\{\alpha_n(b_n)\}\in \overline{C'_{k+1}}$ であるから、$\alpha_n(b_n)\rightarrow q\in \overline{C'_{k+1}}$ である。 $q\ne p_k$ のとき、$p_{k+1}:=q$ とおく。 このとき、$p_k\le p_{k+1}$ である。
以上の処方により得られる点列 $p=p_0<p_1<\cdots<p_k<\cdots$ が極限点列である。 さらに極限点列 $\{p_k\}$ が無限列のときは $\{p_k\}$ は収束しないことが以下のように分かる。
もし $p_k\rightarrow q$ なら $q\in C'\in\mathfrak{R}'$ となる $C'$ が存在し、$C'$ は $\{p_n\}$ の点を無限個含む。 $\mathfrak{R}'$ は局所有限であるから、$C'\cap D\ne\emptyset$ となる $D\in\mathfrak{R}'$ は有限個である。 それらを $\{C'=C'_0,C'_1,\cdots,C'_l\}$ とする。 $C'$ に含まれる各 $\{p_n\}$ に対して、$C_i$ のどれかが選ばれているから、少なくとも一つは無限回選ばれている。 もし $C'$ が無限回選ばれているなら、$\partial C'$ に無限個の部分列 $\{p_{k_n}\}$ が存在し、$p_{k_n}\rightarrow p'\in\partial C'$ となるが、これは $p_k\rightarrow q\in C'$ に矛盾する。 従って、$C'$ が無限回選ばれていることはない。 しかし、これは選び方の基準 $(\ast)$ に矛盾する。
以上により以下の定理を得る。
定理 18 (擬極限曲線の存在)
$(M,g)$ を時空とし、$\{\alpha_n\}:[0,b_n)\rightarrow M$ を以下の2つの条件を満たす未来向きcausal曲線の列とする。
(i) $\lim_n\alpha_n(0)=p\in M$
(ii) $p$ のある近傍 $V$ が存在し、$\alpha_m([0,b_m))\subset V$ となる $m$ は有限個である
凸被覆 $\mathfrak{R}$ とその局所有限な細分 $\mathfrak{R}'$ を任意に定める。 このとき、$\mathfrak{R},\mathfrak{R}'$ に関する $\{\alpha_n\}$ の極限点列 $$p=p_0<p_1<p_2\cdots$$ で次の(i),(ii)を満たすものが存在する。
(i) 各 $p_i$ に対して、部分列 $\{\alpha_m\}:[0,b_m)\rightarrow M$ が存在し、 $$ \begin{align} \alpha_1(s_{1,0})<\alpha_1(s_{1,1})<&\cdots<\alpha_1(s_{1,i}),\\ \alpha_2(s_{2,0})<\alpha_1(s_{2,1})<&\cdots<\alpha_1(s_{2,i}),\\ &\vdots\\ \alpha_m(s_{m,0})<\alpha_m(s_{m,1})<&\cdots<\alpha_m(s_{m,i}),\\ {}^\exists s_{m,l}\in\mathbb{R},\ 1\le m,\ &0\le l\le i, \end{align} $$ となり、かつ任意の $j<i$ に対して、
(a) $\lim_m\alpha_m(s_{m,j})= p_j$
(b) $p_j,p_{j+1}\in {}^\exists C_j\in\mathfrak{R}$
(c) $\alpha_m([s_{m,j},s_{m,j+1}])\subset C_j$
が成り立つ。
(ii) 極限点列 $\{p_n\}$ が無限列なら収束せず、従って擬極限曲線は延長不可能である。
因果的凸近傍
擬リーマン多様体において、近傍 $C$ の任意の2点を結ぶ $C$ に含まれる測地線がただ一つ存在するとき $U$ を測地的凸近傍と呼んだ。測地的凸近傍の因果的性質に関する類似がcausally convex近傍(因果的凸近傍)である。
定義 19
時空 $(M,g)$ において、近傍 $U,V,\ V\subset U$ に対して、$V$ の2点を結ぶ $U$ に含まれるcausal曲線が $V$ に含まれるとき、$V$ は $U$ の中で因果的凸であるという。 特に、$U=M$ のとき、$V$ は因果的凸近傍であるという。
次の定理は適当に小さな近傍の中で因果的凸となる近傍が存在することを主張する。
定理 20
時空 $(M,g)$ の任意の点 $p$ に対して、適当な近傍 $U\ni p$ があり、$p\in V\subset U$ となる近傍 $V$ で $U$ の中で因果的凸となるものが存在する。
Proof.
$p$ の正規近傍 $(U,\{x^0,x^1,\cdots,x^n\})$ を取る。 今、$g_p=-(dx^0)_p^2+\sum_(dx^i)_p^2$ である。 $U$ 上で平坦な計量 $g^+:=-4(dx^0)_p^2+\sum_(dx^i)_p^2$ を定義すると、$T_pM$ の $g_p$ に関してcausalなベクトルは $g^+_p$ に関してtimelikeである。 $g,g^+$ の連続性より必要なら $U$ を小さく取り直すことで、$U$ 上で $g$ に関するcausalベクトルが $g^+$ に関するtimelikeベクトルになるようにできる。 十分小さい $\epsilon>0$ に対して、$p^+:=(\epsilon,0,\cdots,0),\ p^-:=(-\epsilon,0,\cdots,0)$ とするとき、$V:=I_{g^+}^-(p^+)\cap I_{g^+}^+(p^-)\subset U$ となる。 ここで $I^\pm_{g^+}$ は $g^+$ に関するchronological future, pastである。 $g^+$ は平坦であるから $V$ は $U'$ の中で $g^+$ に関して因果的凸である(Minkowski時空の因果的性質)。 $U$ 上で $g$ に関するcausal曲線は $g^+$ に関するtimelike曲線であるから、$V$ は $U$ の中で $g$ に関して因果的凸である。
□次の系は任意の時空の任意の点の近傍で成り立ち、因果構造を論じるのにしばしば有用である。
系 21
時空 $(M,g)$ の任意の点 $p$ に対して、適当な近傍 $U\ni p$ があり、$p\in V_n\subset U$ となる近傍の族 $\{V_n\}$ で $\bigcap_nV_n=\{p\}$ かつ $U$ の中で因果的凸となるものが存在する。
Proof.
上の証明で、$p^+_n:=(\epsilon/n,0,\cdots,0),\ p^n_-:=(-\epsilon/n,0,\cdots,0)$ とするとき、$V_n:=I_{g^+}^-(p^+_n)\cap I_{g^+}^+(p^-_n)\subset U$ と定義すればよい。
□Non-totally vicious時空
時空 $(M,g)$ の任意の点 $p$ を通る区分的 $C^1$ 級時間的閉曲線(closed timelike curve, CTC)が存在するとき、$(M,g)$ をtotally vicious(全悪質)時空という。 CTCは物理的には好ましくない状況が多いが、Gödel宇宙といった相対論でも重要な時空も例としてある。 totally viciousでない時空をnon-totally vicious(非全悪質)時空という。
Chronological時空
Non-totally vicious時空には区分的 $C^1$ 級CTCが存在する場合がある。
定義 22 (chronological時空の定義)
区分的 $C^1$ 級CTCが存在しない時空をchronological(年代順)時空という。
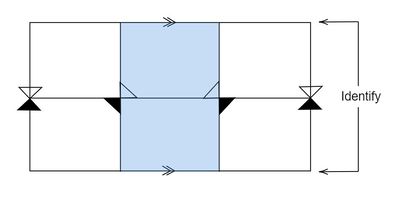
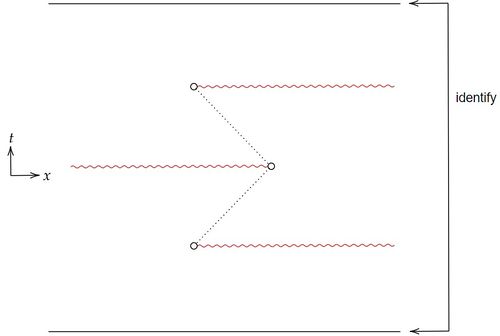
例 23 (non-totally vicisouだがchronologicalでない時空の例)
下図は、Non-totally viciousだがChronologicalではない時空の例である。 白と黒の三角形が光円錐で、白が未来向き、黒が過去向きを表している。
Chronological時空は体積関数を用いて特徴付けることが出来る。
命題 24 (chronological時空の特徴付け)
時空 $(M,g)$ がchronologicalであるための必要十分条件は、$t^\pm$ が任意の未来向きtimelike曲線に沿って狭義単調増加関数となることである。
Proof.
$t^\pm$ が任意の未来向きtimelike曲線に沿って狭義単調増加関数であれば、chronologicalであることは自明である。 逆に、chronological時空であるとする。 もし $p<<q$ なる2点 $p,q\in M$ に対して、$t^-(p)=t^-(q)$ とする。 $I^-(q)\supset I^-(p)$ であるから、$I^-(q)\cap I^+(p)(\subset I^-(q))$ は測度0集合を除いて $I^-(p)$ に含まれる。 従って、$r\in I^-(q)\cap I^+(p)\cap I^-(p)$ が存在し、$p<<r<<p$ となる。 これはchronologicalであることに矛盾する。 $t^+$ に関しても同様である。
□Causal時空
chronological時空には区分的 $C^1$ 級CTCは存在しないが、閉じたcausal曲線は存在する可能性はある。
定義 25 (causal時空の定義)
閉じた区分的 $C^1$ 級causal曲線が存在しない時空をcausal時空と呼ぶ。
chronologicalだがcausalでない時空には定義より閉causal曲線が存在するが、実は次の定理が成り立つ。
定理 26
chronologicalであり、かつcausalではない時空に存在する閉causal曲線は閉null測地線である。
Proof.
もし共役点を持たない $C^1$ 級null測地線でないならその変分曲線でtimelikeなものが存在するため(Lorentz幾何における結論)、chronologicalであることに矛盾する。
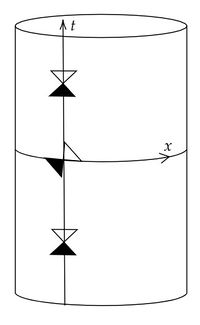
□例 27 (chronologicalだがcausalでない時空の例)
$\mathbb{R}\times S^1$ に計量 $ds^2=(\cosh^2t-1)(-dt^2+dx^2)+2dtdx$ を入れる。 ただし、$t$ は $\mathbb{R}$ の座標で、$x$ は $S^1$ の座標で周期的に同一視をしれておく。 $(\cosh^4t-2\sinh^2t)\nabla_{\partial_x}\partial_x=\cosh t\sinh t^3t\partial_t-\cosh t\sinh t\partial_x$ であるから、$t=0$ のときは $x-$曲線はNull測地線である。 また一般に2次元のLorentz多様体のNull測地線には共役点は存在せず、従ってこのNull測地線と交わるCTCは存在しない(もし存在すれば端点を固定した変分曲線でtimelikeなものが存在することになり、共役点を持たないことに矛盾する)。
chronological時空は $t^\pm$ のtimelike曲線に沿う狭義単調増加性により特徴づけることができた。 しかしcausal時空は同様の方法で特徴づけることはできない。 例えば上の図で中央の閉null曲線から一点を取り除いた時空はcausal時空であるが、このnull曲線に沿って $t^\pm$ は一定である。 この例は $t^\pm$ のcausal曲線に沿う狭義単調増加性によりcausal時空を特徴付けれないことを示している。
Distinguishing時空
causal時空には閉causal曲線は定義より存在しないが、"ほとんど閉じた"causal曲線が存在する可能性はある。 すなわちある点 $p$ と $p$ に任意に近い点 $q$ を結ぶcausal曲線が存在する可能性がある。 このとき、ある点に対してどんなに小さな近傍をとってもその中でのその点の未来、過去が時空全体での未来、過去の区別と一致しないことが起きる。 このようなことを規制するための性質がDistinguishing時空の定義である。 Distinguishing時空の定義として同値な特徴づけが3つある。 これらの同値性は定義を述べてから証明する。
定義 28 (distinguishing時空の定義)
時空 $(M,g)$ がfuture (resp. past) distinguishing(未来区別、過去区別)であるとは、次の同値な3つの条件を満たすときを言う。
(1) 任意の $p\in M$ と任意の近傍 $U(\ni p)$ に対して、$U$ に含まれる $p$ の近傍 $V$ があり、任意の未来向き(resp. 過去向き)causal曲線 $\gamma:[0,1]\rightarrow M$ で $\gamma(0)=p,\gamma(1)\in V$ となるものが、$\gamma\subset V$ となるときをいう。
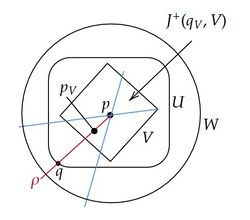
(2) 任意の $p\in M$ と任意の近傍 $U(\ni p)$ に対して、$U$ に含まれる $p$ の近傍 $V$ があり、$J^+(p,V)=J^+(p)\cap V$ (resp. $J^-(p,V)=J^-(p)\cap V$)が成り立つ。
(3) $I^+(p)=I^+(q)$ (resp. $I^-(p)=I^-(q)$) ならば、$p=q$
定理 29 (distinguishing時空の特徴づけ)
上の(1),(2),(3)は同値である。
Proof.
$(1)\Rightarrow(2)$ は自明である。
${\rm non} (3)\Rightarrow {\rm non} (1)$
$p\ne q$ かつ $I^+(p)=I^+(q)$ と仮定する。 $U\ni p$ で $q\notin\bar{U}$ となる $p$ の近傍を任意に1つ取る。 さらに任意に $V\subset U,\ p\in V$ となる近傍 $V$ を1つ取る。 任意の $p'\in I^+(p,V)$ に対して、$I^+(p)=I^+(q)$ であるから、$q$ から出て $p'$ に至る未来向きの時間的曲線 $\gamma_1$ が存在する。 $q'\in\gamma_1,\ q'\notin\gamma_1\cap U$ となる点 $q'$ に対して、$I^+(p)=I^+(q)$ であるから、$p$ から出て $q'$ に至る未来向きの時間的曲線 $\gamma_2$ が存在する。 $\gamma:=\gamma_1\cup\gamma_2$ は $p$ から出て $p'\in V$ に至る時間的曲線であり、作り方から明らかに $V$ に含まれない。
${\rm non} (1)\Rightarrow {\rm non} (3)$
ある点 $p\in M$ に関して(1)が成り立たないとする。 $W\ni p$ を $p$ の凸近傍とし、$U\ni p$ を $W$ に含まれる相対コンパクトな $p$ の近傍とする。 $p$ の近傍の列 $\{V_n\}$ で $U\supset V_n\supset V_{n+1}\ni p,\ \bigcap_n V_n=\{p\}$ かつ $\overline{V}_n$ がコンパクトで $U$ の中で因果的凸であるようなものが存在する。 $p$ に関して(1)が成り立たないから、$p$ から出てさらに $V_n$ からも出て $V_n$ に戻ってくる延長不可能な因果的曲線 $\gamma_n:[0,\infty)\rightarrow M,\ \gamma_n(0)=p$ が存在する。 $V_n$ は $U$ の中で因果的凸であるから $\gamma_n$ は $U$ に含まれない。 $q_n\in \gamma_n\cap\partial U$ を一つ選び点列 $\{q_n\}\in\partial U$ を定める。 ただし、$q_n=\gamma_n(s_n),\ s_n>0$ とする。 さらに、$p_n=\gamma(t_n)\in\gamma_n\cap V_n,\ t_n>s_n>0$ を一つ選び点列 $\{p_n\}\in V_n$ を定める。 このとき $q_n\rightarrow q\in\partial U,\ p_n\rightarrow p$ である。 また $q_n\in J^-(p_n,W)$ であり、$W$ は凸近傍であるから $q\in J^-(p,W)$ である。 よって $I^+(p)\subset I^+(q)$ である。 任意の $q'\in I^+(q)$ に対して、十分大きい $n$ があり、$q_n\in I^-(q')$ となるから $p<<p_n<<q'$ となり、$I^+(p)\supset I^+(q)$ である。 よって $I^+(p)=I^+(q),\ p\ne q$ である。
${\rm non} (1)\Rightarrow {\rm non} (2)$
$p\in U\subset W,\ q\in\partial U$ を上の証明における $U,W,q$ とする。 (2)を満たす近傍 $V(\subset U)$ が存在すると仮定して矛盾を導く。 $q\in J^-(p,W)$ であり、$W$ は凸近傍であるから、$p,q$ を結ぶ $W$ に含まれる時間的測地線 $\rho$ がただ一つ存在する。 このとき、$q_V\in (V\cap\rho)\backslash{p}$ を任意に取ると、$I^+(p)=I^+(q_V)$ である(なぜなら、$I^+(p)\subset I^+(q_V)$ は $q_V$ の作り方から自明であり、(1)を否定している仮定だから、$I^+(p)=I^+(q)$ であり、かつ$q_V\in I^+(q)$ より $I^+(q_V)\subset I^+(q)=I^+(p)$ であるから )。 しかし $U$ は凸近傍であるから $J^+(p,U)\ne J^+(q_V,U)$ であり、特に $J^+(p,V)\not\supset I^+(q_V,V)$ である。 一方、$I^+(q_V,V)\subset I^+(q_V)\cap V=I^+(p)\cap V\subset J^+(p)\cap V$ である。 今、$J^+(p)\cap V=J^+(p,V)$ であるから矛盾である。
□上の定義(1)で $\gamma(1)$ は $V$ の点としか言ってないが $\gamma(0)$ は $p$ でなければならないことに注意。 この後にあるstrongly causal時空の定義では $\gamma(0)\ne p$ でもよい。
例 30 (causalだがdistinguishingでない時空の例)
$\mathbb{R}\times R^2$ に計量 $ds^2=(\cosh^2t-1)(-dt^2+dx^2)+2dtdx+dy^2$ を入れる。 ただし、$t$ は $\mathbb{R}$ の座標で、$x,y$ は $R^2$ の標準的な直交座標である。 この $R^2$ に同値類 $(x,y)\sim(x',y')\Leftrightarrow (x,y+1)=(x',y')\ {\rm or}\ (x+1,y+\alpha)=(x',y'),\ \alpha\in\mathbb{R}\backslash\mathbb{Q}$ を定義し、これによる商時空 $\mathbb{R}\times T^2$ を考える。 これは $x=0$ と $x=1$ を $y$ 方向に $\alpha$ ずらして同一視しているため、$t={\rm const.}$ 面において、$x-$曲線は閉曲線にはならないが $T^2$ の中で稠密である。 特に $t=0$ での $T^2$ において $x-$曲線はnull測地線であり、明らかにdistinguishingでない。 しかし、$T^2|_{t=0}$ の誘導計量は退化しているため、$T^2|_{t=0}$ 中の閉曲線はすべてtimelikeではありえない。 また $T^2|_{t\ne0}$ はspacelike超曲面である。従って、causal時空である。
定理 31 (distinguishing時空の $t^-$ による特徴づけ)
時空 $(M,g)$ がpast (resp. future) distinguishingであることと、$t^-$ (resp. $t^+$) が一般化time functionであることは同値である。
Proof.
一般に $I^-(p)\subset I^-(q)$ であるとき、点列 $\{p_n\}\in I^-(p)$ で $\lim p_n=p$ となるものを取ると、$\gamma_n:[0,1]\rightarrow M$ で $q=\gamma_n(0),p_n=\gamma_n(1)$ となるtimelike曲線が存在し、$\gamma_n$ の極限曲線 $\gamma$ はtimelike曲線である。 任意の $p'\in I^-(p)$ に対して、$I^+(p')\cap I^-(p)$ は無限個の $p_n$ を含むから $p'\in I^-(\gamma([0,1]))$ である。 従って、$I^-(p)\subset I^-(\gamma([0,1]))\subset I^-(q)$ となる。
distinguishing時空でないとすると、$p\ne q$ で $I^-(p)=I^-(q)$ となる $p,q\in M$ が存在する。 上の議論から $I^-(p)\subset I^-(\gamma([0,1]))\subset I^-(q)$ となる。 従って、$I^-(p)= I^-(\gamma([0,1]))= I^-(q)$ となるから、$t^-$ は $\gamma$ 上で一定となり一般化time functionではない。
$t^-$ が一般化time functionでないとすると、$p<<q$ で $t^-(p)=t^-(q)$ となる $p,q\in M$ が存在する。 このとき、$I^-(p)=I^-(q)$ を示せばよい。 $I^-(p)\subset I^-(q)$ は自明だから、逆を示す。 $I^-(q)$ のほとんど全ての点が $I^-(p)$ に含まれるから、点列 $\{q_n\}\subset I^-(p)\cap I^-(q)$ で $\lim q_n=q$ となるものが存在する。 構成より $I^-(q_n)\subset I^-(p)$ であり、$I^-(q)=\bigcup_nI^-(q_n)$ であるから、$I^-(q)\subset I^-(p)$ となる。
□以下はdistinguishing時空の顕著な結果である。
定理 32 (distinguishing時空と共形同値)
$(M_1,g_1),(M_2,g_2)$ を2つのLorentz多様体とし、$(M_1,g_1)$ はdistinguishing時空であるとする。 微分同相写像 $f:M_1\rightarrow M_2$ が任意の $p,q\in M_1$ に対して、$p\le q$ ならば $f(p)\le f(q)$ となるとき、$(M_2,g_2)$ はdistinguishingであり、適当な関数 $\rho\in C^0(M_1)$ があり、$f^\ast g_2=e^{2\rho}g_1$ が成り立つ。
Strongly causal時空
時空の任意の点の十分小さい近傍 $U$ において、$U$ の中で因果的凸となる近傍 $V$ は存在する。 しかし、$U$ を任意に取った場合は因果的凸近傍が存在するとは限らない。 これを保障するのがstrongly causal時空である。 また、“ほとんど閉じた”causal曲線を完全に規制する条件でもある。
定義 33 (strongly causal時空の定義)
時空 $(M,g)$ がある点 $p\in M$ においてstrongly causalであるとは、次の同値な条件のいずれかを満たす時を言う。
(1) $p$ の任意の近傍 $U$ に対して、$p$ の適当な近傍 $V(\subset U)$ で $M$ において因果的凸であるものが存在する。
(2) $p$ の任意の近傍 $U$ に対して、適当な近傍 $V(\ni p)$ があり、任意のcausal曲線 $\gamma:[0,1]\rightarrow M$ で $\gamma(0),\gamma(1)\in V$ ならば、$\gamma\subset U$ となる。
任意の $p\in M$ においてstrong causalであるとき、時空 $(M,g)$ はstrong causalであると言う。
(1),(2)の同値性
$(1)\Rightarrow(2)$ は自明である。 逆に条件(2)が成り立つとする。 $p$ の任意の近傍 $U$ に対して、2つの近傍 $p\in V\subset U'\subset U$ で $V$ が $U'$ の中で因果的凸であるものが存在する。 $U'$ に対して、(2)の条件を満たす近傍として $V$ を取ることが出来る。 このとき $V$ に2つの端点を持つ $M$ のcausal曲線 $\gamma$ は(2)の条件より $U'$ に含まれるが、$V$ は $U'$ の中で因果的凸であるから $\gamma\subset V$ である。 従って、$V$ は $M$ において因果的凸である。
□例 34 (distinguishingだがstrong causalでない時空の例)
下図はdistinguishingだがstrong causalでない時空の例である。
strong causal時空にはAlexandorv位相による特徴付けがある。
定義 35 (Alexandorv位相の定義)
時空 $(M,g)$ において、部分集合族 $$ \begin{align} \mathcal{B}_A:=\{I^+(p)\cap I^-(q);\ p,q\in M\} \end{align} $$ が開基となって定める位相をAlexandorv位相 (Alexandorv topology)という。
位相空間 $(X,O)$ の基とは $X$ 部分集合族 $B$ で $X$ の任意の開集合が $B$ の部分族の和集合となるときを言う。 詳しくは位相空間論3:開基を参照されたい。
定理 36 (strong causal時空のAlexandorv位相による特徴付け)
時空 $(M,g)$ に関して以下は同値である。
(1) $(M,g)$ はstrong causal時空である。
(2) Alexandorv位相は $M$ の元の位相と一致する。
(3) Alexandorv位相はHausdorffである。
Proof.
$(1)\Rightarrow(2)$
$\mathcal{B}_A$ がある位相の開基となっていることはすぐにわかる。 さらに $\mathcal{B}_A$ の元は $M$ の元の位相に関して開集合であるから、$M$ の元の位相はAlexandorv位相より細かい。 任意 $x\in M$ と $x$ の任意の近傍 $U\ni x$ に対して、$(M,g)$ はstrong cuausal時空であるから、$x\in V\subset U$ で $<<_V$ と $<<$ が一致するような近傍 $V$ が存在する。 従って、$p,q\in V$ で $p<<_Vx,\ x<<_Vq$ となる2点に対して $q\in I^-(q)\cap I^+(p)\subset U$ となる。
$(2)\Rightarrow(3)$
自明である。
$(3)\Rightarrow(1)$
待遇を取り、(1)の否定から(3)の否定を導く。 ある点 $p$ がstrongly causalでないとする。 $p$ の凸近傍 $W$ を取り、$W$ に対して相対コンパクトな $p$ の近傍 $U\subset W$ を取る。 さらに必要なら $U$ を小さく取り直し、$U$ の中で因果的凸な $p$ の近傍族 $\{V_n\},\ p\in V_n,\ \bigcap_nV_n=\{p\}$ を取る。 十分大きい $n$ と任意の $p_n,r_n\in V_n$ に対して、$p_n$ から出発し $r_n$ に戻ってくる $W$ に含まれない未来向きのcausal曲線を $\gamma_n$ とする。 $U$ は $W$ に対して相対コンパクトだから $q_n\in\gamma_n\cap\partial U$ は必要なら部分列を取れば $q_n\rightarrow q\rightarrow\partial U$ となる。 $W$ は凸近傍であり、$q_n<<r_n$ かつ $r_n\rightarrow_W p$ であるから、$q<<_Wp$ である。 $q_1<<q<<q_2$ となる任意の $q_1,q_2\in M$ に対して、$q_1<<p$ である。 また十分大きい $n$ に対して、$p_n<<q<<q_2$ である。 $p_n$ を $p<<_{V_n}p_n$ となるように取れば、$p_n\in I^+(q_1)\cap I^-(q_2)$ である。 よって、$p$ は $I^+(q_1)\cap I^-(q_2)$ の集積点であるから、$p$ の任意の近傍は $I^+(q_1)\cap I^-(q_2)$ と交わりを持つ。
□Strongly causal時空の基礎的な性質として次の2つの命題がある。
命題 37
strongly causal時空 $(M,g)$ において、延長不可能なcausal曲線 $\gamma:[0,b)\rightarrow M$ がコンパクト集合 $K$ に対して、$\gamma(0)\in K$ であるならば、ある $s\le b$ があり、$t>s$ となる任意の $t$ に対して、$\gamma(t)\notin K$ となる。
Proof.
結論を否定して矛盾を導く。 結論の否定により、点列 $\{t_n\},\ t_n\rightarrow b$ で $\gamma(t_n)\in K$ となるものが存在する。 $K$ のコンパクト性より必要なら部分列を取り直し $\gamma(t_n)\rightarrow p\in K$ となる。 $\gamma$ は延長不可能でるから別の点列 $\{u_n\},\ u_n\rightarrow b$ で $\gamma(u_n)$ が $p$ に収束しないものが存在しなければならない(もし全ての点列が $p$ に収束すれば定義より延長可能になってしまう)。 必要なら点列の番号を付け替えて、$t_1<u_1<t_2<u_2<\cdots<t_i<u_{i+1}<\cdots<b$ であるとしてよい。 $\gamma(u_n)$ は $p$ に収束しないからある近傍 $U\ni p$ があり、$\gamma(u_n)\notin U$ である。 任意の$p$ の近傍 $V(\subset U)$ に対して、ある $k$ があり、$\gamma(t_k),\gamma(t_{k+1})\in V$ であり、 $\gamma(u_k)\notin U$ である。 これは $p$ がstrongly causalであることに矛盾する。
□命題 38
$(M,g)$ をstrongly causal時空、$K$ をコンパクト部分集合とする。 未来向きのcuasal曲線の列 $\{\alpha_n\}:[0,1]\rightarrow K,\ (\lim\alpha_n(0)=p,\ \lim\alpha_n(1)=q,\ p,q\in K,\ p\ne q)$ に対して、 区分的滑らかな未来向きcausal測地線 $\lambda:[0,1]\rightarrow K,\ \lambda(0)=p,\lambda(1)=q$ で、ある部分列 $\{\alpha_m\}$ があり、$\lim L(\alpha_m)\le L(\lambda)$ となるものが存在する。
Proof.
$\{\alpha_n\}$ の極限点列を $p=p_0\le p_1\le p_2\le\cdots\le p_n=q$ とする($n=\infty$ だと擬極限曲線が延長不可能になり上の命題よりあり得ない)。 擬極限曲線を $\lambda=\bigcup_{i=0}^{n-1}\overrightarrow{p_ip_{i+1}}$ とする。 このとき、$\overrightarrow{p_ip_{i+1}}\subset K$ でかつある凸近傍 $C_i$ があり $\overrightarrow{p_ip_{i+1}}\subset C_i$ となっているとしてよい。 このとき、部分列 $\{\alpha_m\}$ があり、$\alpha_m(s_{m,i}),\alpha_m(s_{m,i+1})\subset C_i$ となっていて、 $$ \begin{align} L(\alpha_m([s_{m,i},s_{m,i+1}]))\le L(\overrightarrow{\alpha_m(s_{m,i})\alpha_m(s_{m,i+1})}) \end{align} $$ である。 ただし、$\overrightarrow{\alpha_m(s_{m,i})\alpha_m(s_{m,i+1})}$ は $\alpha_m(s_{m,i}),\alpha_m(s_{m,i+1})$ を結ぶ未来向き測地線である。 凸近傍内では $L$ は連続であるから、 $$ \begin{align} \lim_{m\rightarrow\infty}L(\alpha_m)\le L(\lambda) \end{align} $$
□注意:擬極限曲線がnull測地線となるようなtimelike曲線の列に対しても上の命題は成立することに注意するべきである。すなわち $\lim_{m\rightarrow\infty}L(\alpha_m)=L(\lambda)=0$ である。この例から分かるように有限 $m$ に対しては不等式が成立するとは限らない。
次の命題は2次元の特殊さを示す。
命題 39
任意の単連結な2次元時空はstrongly causalである2。
Proof.
□
time separationはRiemann多様体における距離に対応する概念であるが、Lorentz多様体としての等長同型とtime separationが保存されることが一致するのがstrongly causal時空である。
定理 40
$(M,g),(M',g')$ を次元が同じ時空とし、$(M,g)$ をstrongly causal時空とする。 全射 $f:M\rightarrow M'$ が $$ \tau(p,q)=\tau'(f(p),f(q)),\ {}^\forall p,q\in M $$ を満たすならば、$f$ は等長同型写像である。 特に $M=M'$ ならばtime separationが一致するのは計量が一致するときに限る。 ここで、$\tau,\tau'$ はそれぞれ $(M,g),(M',g')$ のtime separationである。 また $f$ に対して連続性の仮定は必要ない。
Stably causal時空
causal時空の計量を少し摂動したものもcausal時空になるとは限らない。 もしなるならその時空のcausalという性質は安定であることになる。 これがstably causal時空である3。
まず計量を摂動するということの意味を明確に定義する。 以下に見るように摂動というよりは光円錐を少し“開く”ことに対応する。
時空 $(M,g)$ 上の時間的に向き付けられた計量全体を $Lor(M)$ と書く。 $Lor(M)$ に半順序 $<$ を次のように定める。
$g,g'\in Lor(M)$ に対して、$g$ に関するcausalベクトルが全て $g'$ に関してtimelikeになるとき、$g<g'$ と定める。
定義 41 (stably causal時空の定義)
時空 $(M,g)$ がstably causal時空 (安定的因果時空) であるとは、計量 $g'$ で $g<g'$ となり、かつ $(M,g')$ がcausal時空となるものが存在するときを言う。
$g_1<g_2$ であるとき、$g_\lambda:=\lambda (1-\lambda)g_1+\lambda g_2>g_1,\ (0\le\lambda\le1)$ であることが簡単に分かる。
stably chronologicalも同様に定義される。 次の命題から分かるようにstably causalとstably chronologicalを区別する必要はない。
命題 42
stably causalとstably chronologicalは同値である。
Proof.
stably causalならば明らかにstably chronologicalである。 逆を示すには、stably causalでないならばstably chronologicalでないことを示せばよい。 $(M,g)$ がstably causalでないならば、任意の $g_1>g$ となる計量 $g_1$ に対して、 $g_1>g_2>g$ となる計量 $g_2$ を取ると $g_2$ に関して閉causal曲線 $\gamma$ が存在する。 定義より $\gamma$ は $g_1$ に関して閉chronological曲線である。 よって $(M,g_1)$ はchronologicalでない。
□2次元時空はいくらかの側面で特別であり以下はその特別性の一つを示している。
命題 43
単連結な2次元時空はstably causalである。
Proof.
任意の単連結な2次元時空はstrongly causalであり、従ってcausalであることから分かる。
□stably causal時空の特徴づけとして次の定理がある。 これはstably causalの定義からは全く明らかでなく特筆すべき性質である。
定理 44 (stably causal時空の特徴付け)
時空 $(M,g)$ に対して以下は同値である。
(1) stably causalである。
(2) time functionが存在する。
(3) temporal functionが存在する。
Proof.
この定理の証明は長いので概略のみ示す。 詳しくは3,4を参照されたい。
(3)$\Rightarrow$(1)
temporal functionを $T:M\rightarrow\mathbb{R}$ とする。 stably causalという性質は因果的な構造なので共形不変である。 従って適当に共形変換して、$g(\nabla T,\nabla T)=-1$ として、$g=-dT^2+h$ としてよい。 $h$ は $T=const.$ で定義される滑らかな空間的部分多様体に誘導されたリーマン計量である。 このとき、$g_\lambda:=-\lambda dT^2+h,\ \lambda>0$ という計量の族を考えると、$(M,g_\lambda)$ においても $T$ はtemporal functionであるからcausal時空である。 $1<\lambda$ に対して、$g<g_\lambda$ であるからstably causalである。
(1)$\Rightarrow$(2)
$g<\tilde{g}$ でcausalとなる $\tilde{g}$ を一つ取る。 計量の族 $g_\lambda:=g+\frac{\lambda}{2}(\tilde{g}-g),\ 0\le\lambda\le2$ を考えると、$g_\lambda$ は全てcausalである。 $t^-_\lambda$ を $g_\lambda$ に関する過去体積関数とする。 $t^-_\lambda$ を積分して $$ t(p):=\int^1_0t^-_\lambda(p)d\lambda $$ を定義すると、これが $(M,g)$ に関してtime functionとなっていることを確かめることができる。
(2)$\Rightarrow$(3)
4による。
□またstably causal時空の全体はstrongly causal時空の全体の部分集合であることが次の命題から分かる。
命題 45
stably causal時空はstrongly causal時空である。
Proof.
time functionを $t$ とする。 任意の点 $p\in M$ と任意の近傍 $U(\ni p)$ が与えられたとき、$p$ の凸近傍 $C_1\subset U$ を取る。 さらに $p$ の凸近傍 $C_2$ で $C_2\subset C_1$ かつ $C_1$ に対して相対コンパクトとなるものを取る。 $t(p)=0$ としてよい。 $q\in C_2$ に対して $\epsilon^+(q):=\min\{t(r);\ r\in J^+(p,C_1)\cap \partial C_2\},\ \epsilon^-(q):=\min\{|t(r)|;\ r\in J^-(p,C_1)\cap \partial C_2\}$ とし、$\epsilon(q):=\min\{\epsilon^+(q),\epsilon^-(q)\}$ と定義する。 $C_1$ 内では $J^\pm$ は連続であり、$\partial C_2$ はコンパクトであるから、$\epsilon(q)$ は連続である。 $p\in W\subset C_2$ となり $C_2$ に対して相対コンパクトとなる近傍 $W$ を取り、$\epsilon_W:=\min\{\epsilon(r);\ r\in W\}$ とする。 $V:=W\cap t^{-1}((-\epsilon_W/2,\epsilon_W/2))$ と置く。 今、$V$ の点を始点とするcausal曲線 $\gamma$ で $U$ を出ていくものは $C_1$ を出ていくからある点 $p'$ において $t(\gamma(p'))>\epsilon_W$ または $t(\gamma(p'))<-\epsilon_W$ となり、$t$ はtime functionであるから $\gamma$ が $V$ に戻ってくることは不可能である。 よって近傍 $V$ は $U$ に対してstrongly causal時空の定義(2)を満たす。
□次の例はstrongly causalであるがstably causalではない時空である。 このことからstably causal時空の全体がstrongly causal時空の全体の真部分集合である。
Causally continuous時空
stably causal時空にはtime functionが存在した(さらにtemporal functionの存在も同値であった)。 しかしstably causal時空でも体積関数 $t^-$ がtime functionとなるとは限らない。 一般に $t^-$ は連続ではないからである。 $t^-$ が連続となるときは時空の因果構造、特に因果錐が連続であると理解することができるだろう。 distinguishing時空では $t^-$ が一般化time functionであったことを思い出すと次のように定義する。
定義 46 (causally continuous時空)
時空 $(M,g)$ がcausally continuous時空であるとは、以下の同値な条件を満たすことである。
(1) $(M,g)$ はdistinguishingであり、かつ $t^\pm$ が連続である。
(2) $t^\pm$ はtime functionである。
これらが同値なことはdistinguishing時空の特徴づけから明らかである。 またstably causal時空の特徴づけから次も明らかである。
命題 47
causally continuous時空はstably causal時空である。
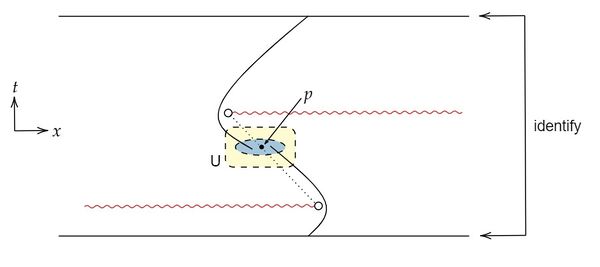
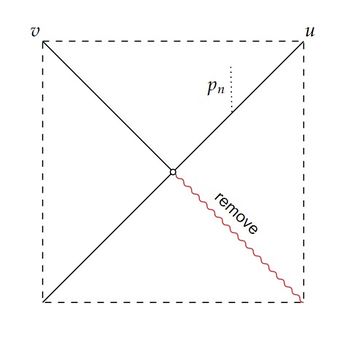
例 48 (stably causalだがcausally continuous時空でない時空の例)
下図のようなMinkowski時空の開部分多様体を考える。 原点及び赤色の波線部分は取り除かれているとする。 このとき、例えば点列 $\{p_n\}$ を考えれば分かるように、明らかに $t^-$ は連続でない。
Causally simple時空
定義 49 (causally simple時空)
時空 $(M,g)$ が causally simple (因果的単純) 時空であるとは、(i) causalでかつ (ii) 任意の $p\in M$ に対して、$J^\pm(p)$ が閉集合となることである。
上の定義で(i)の条件をdistinguishingにした定義もある。 しかし以下の命題から分かるように上に定義された時空はdistinguishingである。 従って2つの定義は同値である。
命題 50
(上の定義の意味で)causally simple時空はdistinguishingである。
Proof.
distinguishingでないと仮定して矛盾を導く。 $p\ne q$ で $I^+(p)=I^+(q)$ となる $p,q$ があるから、点列 $\{q_n\},\ q_n\rightarrow q,\ q<<q_n$ を考えると、$q\in \overline{I^+(q)}=\overline{I^+(p)}=\overline{J^+(p)}=J^+(p)$ となる(左から1つ目の等号はdistinguishingでない時空で常に成り立ち、2つ目の等号は任意の時空で成り立ち、3つ目の等号は(ii)の仮定より成り立つ)。 よって $p<q$ である。 同様に $q<p$ である。 従ってcausal時空でなくなり矛盾する。
□この命題の証明からdistinguishingでなく、$J^+$ が閉である時空はcausal時空でないことも分かる。
次の命題はcausally simple時空がcausally continuous時空の部分集合であることを示している。
命題 51
causally simple時空はcausally continuous時空である。
Proof.
reflectivityを示す。 $q\in \overline{I^\pm(p)}=J^\pm(p)$ とすると、$p\in J^\mp(q)=\overline{I^\mp(q)}$ である。
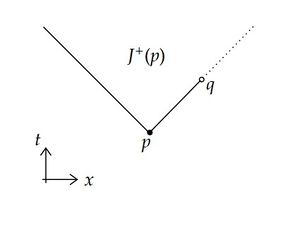
□例 52 (causally continuousだがcausally simpleでない時空の例)
2次元Minkowski時空から一点を取り除いた時空はcausally continuousであるが、causally simpleでない。 実際、下図において $J^+(p)$ は閉集合でない。
causaly simple時空の因果構造はこれまでの時空に比べればかなり“整っている”が以下の歓迎されない性質を持つことがある。
(1) ある $p,q$ に対して、$\tau(p,q)=\infty$ となることがある。
(2) $\tau(p,q)<\infty$ でも $p,q$ を結ぶcausalな測地線が存在しないことがある。
(3) $\tau$ が連続でないことがある。
例 53 (causally simple時空で上の(1),(2),(3)が成り立つ例)
下図は $\mathbb{R}^2$ から斜線部を取り除いた開部分多様体に適当なLorentz計量を入れた時空である。 計量が $g=-dt^2+dx^2$ のとき、$\tau(p,q)=2$ だが $p,q$ を結ぶcausalな測地線は存在しない。 計量が $g=\frac{1}{x^2+t^2}(-dt^2+dx^2)$ のとき、$\tau(p,q)=\infty$ である。 計量が $g=\frac{1}{(1+x)^2}(-dt^2+dx^2)$ のとき、$\tau(p,q)<\infty$ であるが、$q\le q'$ となる任意の $q'$ に対して、$\tau(p,q')=\infty$ となるから $\tau$ は不連続である。
Globally hyperbolic時空
globally hyperbolic時空が因果階層の中で一番狭いクラスである。 この時空の性質は物理的に見て極めて自然な要請である。 また数学的にはリーマン多様体におけるコンパクト多様体に類似の地位を占めておりしばしば扱いやすい時空である。 ここではglobally hyperbolic時空の定義やいくつかの有名な事実をまとめる。 証明は長くなるためGlobally Hyperbolic時空を参照されたい。
定義 54 (globally hyperbolic時空)
時空 $(M,g)$ がglobally hyperbolic(大域双曲的)であるとは、(i) causalであり、(ii) 任意の $p,q\in M$ に対して、$J^+(p)\cap J^-(q)$ がコンパクトとなることである。
命題 55
globally hyperbolic時空はcausally simple時空である。
Proof.
任意の $p\in M$ に対して、$J^\pm(p)$ が閉であることを示せばよい。 $q\in \overline{J^+(p)}$ に対して、点列 $\{q_n\}$ で $q_n\rightarrow q$ かつ $q_n\in J^+(p)$ となるものを取ることが出来る。 $r\in I^+(q)$ に対して、$I^-(r)$ は $q$ の近傍であるから $\{q_n\}\in I^-(r)$ としてよい。 よって $\{q_n\}\in J^+(p)\cap J^-(r)$ であるからglobally hyperbolicの仮定より $q_n\rightarrow q\in J^+(p)\cap J^-(r)\subset J^+(p)$ である。 従って、$\overline{J^+(p)}\subset J^+(p)$ である。
□上の証明から分かるように、定義の条件(ii)が成り立てば $J^\pm$ は閉である。 条件(i)を単にcausalとした場合でもcausally simple時空となりstrongly causal時空であることが分かる。 従って条件(i)はcausalでもstrongly causalでもどちらでもよいし、strongly causalという条件は少し冗長であるからcausalとした方が経済的である。 しかし、条件(i)としてstrongly causalが採用されることが多い。
時空のあるachronalな位相的超曲面 $S$ 上で場の初期条件を定めた時、それが時間発展して $S$ より未来の時空領域の任意の点における場の値が一意的に定まるという状況は物理的にはごく自然なことである。 globally hyperbolic時空はこのような性質を持つ時空としても特徴づけることができる。
定義 56 (domain of dependence)
$(M,g)$ を時空として、$A$ をachronal部分集合とする。 $A$ のfuture domanin of dependence(未来依存領域)$D^+(A)$ とは、$M$ の点 $p$ で $p$ を通る全ての延長不可能な過去向き時間的曲線が $A$ と交わるという性質を満たすものの集合である。 past domanin of dependence $D^-(A)$ も過去と未来を入れ替えて同様に定義する。 $D(A):=D^+(A)\cup D^-(A)$ を $A$ のdomain of dependenceという。
future domain of dependenceは $A$ の情報のみから古典論的に完全に予測し得る時空の領域である。
定義 57 (Cauchy horizon)
achronal set $A\subset M$ に対して、$A$ のfuture Cauchy horizon(未来Cauchy地平面) $H^+(A)$ は $H^+(A):=\overline{D^+(A)}\backslash I^-(D^+(A))$ と定義される。 past Cauchy horizon $H^-(A)$ も同様である。 $H(A):=H^+(A)\cup H^-(A)$ を $A$ のCauchy horizonと呼ぶ。
achronal set $A$ が閉集合のときは、$\partial D^+(A)=H^+(A)\cup A$ である。
以下に定義するCauchy超曲面はこの集合(位相的超曲面となる)の情報のみから古典論的に時空全体を完全に予測することのできるものである。
定義 58 (Cauchy超曲面)
時空 $(M,g)$ のCauchy超曲面とは次の同値な条件を満たす $M$ の部分集合 $S$ のことである。
(i) $M$ の任意の延長不可能な時間的曲線は唯一点において $S$ と交わる。
(ii) $S$ はachronalで $D(S)=M$.
(iii) $S$ はachronalで $H(S)=\emptyset$.
Cauchy超曲面 $S$ は次の性質を持つことが知られている。 $S$ は閉集合であり、位相的超曲面である。 $M=I^+(S)\coprod S\coprod I^-(S)$ である。 $S$ が空間的な場合は任意の延長不可能な因果的曲線と唯一点で交わる(このとき $S$ は少なくとも $C^1$ 級である)。 コンパクト集合 $K$ に対して、$J^\pm(K)\cap S$ はコンパクトである。
関数 $t:M\rightarrow\mathbb{R}$ が ある $c\in\mathbb{R}$ に対して、$S=t^{-1}(c)$ を満たすとき $t$ はCauchyであるという。
次の定理はGerochにより示された顕著な結果である。
定理 59 (globally hyperbolic時空のCauchy超曲面による特徴づけ)
時空 $(M,g)$ がglobally hyperbolicであることとCauchy超曲面 $S$ を持つことは同値である。 さらにこのとき、Cauchy time functionが存在し、また任意のCauchy超曲面は $S$ と同相であり、$M$ は $S\times\mathbb{R}$ と同相である。
出典
- 3.a 3.b Sánchez, Miguel.. (2004) "Causal hierarchy of spacetimes, temporal functions and smoothness of Geroch's splitting. A revision.". arXiv preprint gr-qc/0411143 (2004) .
- 4.a 4.b Bernal.A.N. and Sánchez.M.. (2005) "Smoothness of time functions and the metric splitting of globally hyperbolic spacetimes.". Commun. Math. Phys. 257, 43–50 .