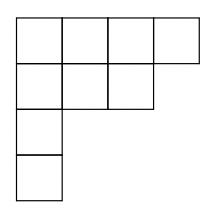
Young図形
提供: Mathpedia
正の整数列 $ \lambda=(\lambda_1,...,\lambda_\ell) $ が 2次元Young図形であるとは, $$ \lambda_{i}\geq \lambda_{i+1},\quad{}i=1,...,\ell-1 $$ が満たされることをいう. また, 次の記号がよく用いられる: $$ |\lambda|:=\sum_{i=1}^{\ell}\lambda_i $$ 2次元Young図 $\lambda$ は, $|\lambda |$という数の分割である, ともいう.
例 右の画像は, $\lambda=(4,3,1,1)$という2次元Young図であり, $|\lambda|=4+3+1+1=9$ である.
分割の母関数
次の等式が知られている:
$$ \sum_\lambda q^{|\lambda|}=\prod_{n=1}^{\infty} \frac{1}{1-q^n} $$
2次元Young図は, 表現論においてしばしば用いられる図形であり, 理論物理学においても様々なところで現れることが知られている.