Newton法
[math] \newcommand\eps\varepsilon{} [/math]
Newton法
Newton法(ニュートンほう)とは、関数の零点を近似的に得るために用いられる反復計算法の一つである。代数方程式の求根についてNewton−Raphson法(ニュートン−ラフソンほう)、一般の関数についてNewton−Raphson−Simpson法(ニュートン−ラフソン−シンプソンほう)と呼ばれることもあるが、本稿では単にNewton法と呼ぶ。
形式的な定義
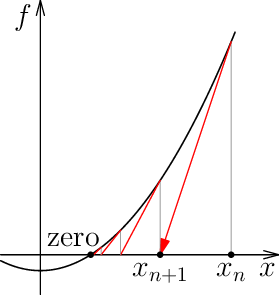
$X$ をBanach空間、$f \colon X \to X$ をFréchet微分可能な写像とする。このとき、$x_0 \in X$ を初期値とするNewton法とは、次の漸化式で定義される数列を求めることおよびこの漸化式による反復計算手法を指す。 $$x_{n+1} = x_n - Df_{x_n}^{-1} f(x_n).$$ ここで、$Df_x \colon X \to X$ は $f$ の $x \in X$ におけるFréchet微分を表す。漸化式の定義における有界線形作用素の逆作用素 $Df_x^{-1}$ は一般には存在するとは限らないことに注意する。
数列のwell-defined性と収束性
以下では、簡単のためEuclid空間 $X = \mathbb{R}^n$ を考え、Newton法による数列のwell-defined性および収束性を証明する。
定理 0 (Newton法の収束性)
$f$ の零点 $x$ が存在し、$x$ のある近傍 $U$ ($\subset X$) で $f$ が一階連続的微分可能であって、$U$ の各点において $f$ のヤコビ行列が可逆であると仮定する。このとき、以下を満たすような $x$ の近傍 $U' \subset U$ が存在する。
- 任意にとった $x_0 \in U'$ を初期値とするNewton法による数列 $(x_n)_n$ がwell-definedであって、
- 初期値の取り方に関わらずその収束先が常に $\lim_{n \to \infty} x_n = x$ である。
Proof.
$N$ を $f$ の"Newton写像"とする: $$N \colon U \to X, \qquad N(y) = y - Df_y^{-1} f(y).$$ $\eps(y) = y - x$ とおくと、 $$\eps(N(y)) = N(y) - x = \eps(y) - Df_{y}^{-1} f(y)$$ が成り立つ。ここで $f$ が一階微分可能であることから、Taylorの定理より $$f(y') = f(y) + Df_{y}(y' - y) + h(y';y)|y'-y|, \qquad \lim_{y' \to y} h(y'; y) = 0$$ なる剰余項 $h$ がとれ、$y' = x$ を代入して $$\eps(N(y)) = \eps(y) - Df_{y}^{-1} \left[ Df_{y}\eps(y) - h(x; y)|x-y| \right] = Df_{y}^{-1} h(x; y) | \eps(y)|$$
を得る。$f$ の滑らかさと剰余項の性質より $|Df_{y}^{-1} h(x; y)|$ は $y$ について連続関数で、閉球 $B_\delta(x) = \{y \mid |x - y| \le \delta\}$ の上で最大値 $M$ を持つ。ただし、$B_\delta(x) \subset U$ となるよう半径 $\delta \gt 0$ をとった。このとき、直ちに $|\eps(N(y))| \le M|\eps(y)|$ が従う。ゆえに、$M \lt 1$ が成り立つよう $\delta$ を小さく取り直せばNewton写像 $N$ が閉球 $B_\delta(x)$ の上で縮小写像となり、いかなる初期値 $x_0 \in B_\delta(x)$ に対しても $N^n(x_0)$ の収束先が $x$ となることがわかる。最後に、$\delta$ は $f$ のみに依存して定まる定数であったので、近傍としてはこの閉球 $U' = B_\delta(x)$ を選べば良い。(Q.E.D.)系 1 (Newton法の二次収束性)
$f$ にさらに二階微分可能性を課せば、定理 0の証明におけるTaylor剰余項として二次の項をとることができ、$|\eps(N(y))| \le |\eps(y)|^2$が成り立つ。すなわち、Newton法による反復誤差評価が $$|x_{n+1} - x| \le |x_n - x|^2$$ で与えられる。
以上のことから、$f$ が十分滑らかで初期値 $x_0$ を零点 $x$ の十分近くにとれば、Newton法の収束は極めて速いことがわかる。
補足
証明から直ちに分かるように、Taylorの定理が成り立つような一般の位相線形空間の枠組みにおいても同様の評価を示すことができる。
$x$ が $f$ の零点である $f(x)=0$ ことと、$x$ が $N$ の不動点である $x = N(x)$ ことは同値である。よって、零点の存在を仮定した上で縮小写像の原理(Banachの不動点定理)を用いて収束性を示したが、逆に $N$ に対して不動点定理(Brouwerの不動点定理やSchauderの不動点定理でも良い)を用いることで $f$ の零点が存在するための十分条件を調べることもできる。