有限オートマトン
[math] \newcommand{\mathsetextension}[1]{% \left\{ #1 \right\}% } \newcommand{\mathsetintension}[2]{% \left\{ #1 \left| #2 \right. \right\}% } \newcommand{\mathof}[2]{% \mathop{#1}\left(#2\right)% } \newcommand{\mathpowerset}[1]{% 2^{#1}% } \newcommand{\mathderiv}{\mathrel{\mathop{\Rightarrow}}^{*}} \newcommand{\mathgen}{\rightsquigarrow} \newcommand{\emptyword}{\varepsilon} \newcommand{\kleenecl}[1]{{#1}^{*}} \newcommand{\interpret}[1]{[\![#1]\!]} \newcommand{\mathautomaton}[1]{\mathcal{#1}} \newcommand{\mathnat}{\mathbb{N}} \newcommand{\qed}{\blacksquare} [/math]
有限オートマトン(finite automaton)とは正規言語を受理する計算モデルである。
以下、項目形式言語において定められている言語上の演算などについては特に断らず用いる。
有限オートマトンの導入
この節では有限オートマトンやその周辺の重要な諸概念を定義する。
定義 1 (有限オートマトン)
有限オートマトン(finite automaton)とは
- 状態集合(a set of states)と呼ばれる有限集合 $Q$
- 記号集合 $\Sigma$
- 遷移関係(transition relation)と呼ばれる集合 $\Delta \subseteq Q\times (\Sigma \cup \mathsetextension{\emptyword}) \times Q$
- 開始状態(initial state)と呼ばれる $q_{I}\in Q$
- 受理状態(accepting state)や最終状態(final state)と呼ばれる集合 $F\subseteq Q$
の5つ組 $(Q, \Sigma, \Delta, q_{I}, F)$ である。
定義 2 (有限オートマトンの受理する言語)
有限オートマトン $\mathautomaton{A}=(Q, \Sigma, \Delta, q_{I}, F)$ と 記号列 $w \in \kleenecl{\Sigma}$ について、 次の2条件を満たす状態の列 $q_{0}, q_{1}, \dots, q_{n}$ を 記号列 $w$ による $q_{0}$ から $q_{n}$ への $\mathautomaton{A}$ の状態遷移と言う。
- $w=a_{1}a_{2} \dots a_{n}$ (ただし、各 $i=1, \dots, n$ について $a_{i}\in \Sigma\cup\{\emptyword\}$)
- すべての $i\in \{1, \dots n\}$ について $(q_{i-1}, a_{i}, q_{i})\in \Delta$
記号列 $w$ による $\mathautomaton{A}$ の状態遷移 $q_{0}, q_{1}, \dots, q_{n}$ であって $q_{0} = q_{I}$, $q_{n}\in F$ を満たすものが存在するとき、 「有限オートマトン $\mathautomaton{A}$ が 記号列 $w$ を受理する」と言う。
有限オートマトン $\mathautomaton{A}$ が受理する 記号列全体のことを 有限オートマトン $\mathautomaton{A}$ の受理する言語 と言い、$L(\mathautomaton{A})$ と書く。
定義 3 (等価な有限オートマトン)
有限オートマトン $\mathautomaton{A}$ と 有限オートマトン $\mathautomaton{A'}$ が等価であるとは、 $L(\mathautomaton{A})=L(\mathautomaton{A'})$ を満たすことである。
有限オートマトンの例
この節では有限オートマトンの例を紹介する。
例 4 ($0$ と $1$ からなる有限記号列全体を受理する有限オートマトン)
\begin{align*}Q&=\mathsetextension{q_{I}}\\ \Sigma&=\mathsetextension{0, 1}\\ \Delta&=\mathsetextension{(q_{I}, 0, q_{I}), (q_{I}, 1, q_{I})}\\ F&= \mathsetextension{q_{I}}\end{align*} とすると、$\mathautomaton{A}=(Q, \Sigma, \Delta, q_{I}, F)$ は有限オートマトンである。また、$\mathautomaton{A}$ は決定性有限オートマトンである。
この有限オートマトン $\mathautomaton{A}$ は $0$ と $1$ からなる有限記号列をすべて受理する。
例 5 ($0$ と $1$ のみを受理する有限オートマトン)
\begin{align*} Q&=\mathsetextension{q_{I}, q_{1}, q_{2}}\\ \Sigma&=\mathsetextension{0, 1}\\ \Delta&=\mathsetextension{(q_{I}, 0, q_{1}), (q_{I}, 1, q_{1}), (q_{1}, 0, q_{2}), (q_{1}, 1, q_{2})}\\ F&=\mathsetextension{q_{1}} \end{align*} とすると、$\mathautomaton{A}=(Q, \Sigma, \Delta, q_{I}, F)$ は有限オートマトンである。
この有限オートマトン $\mathautomaton{A}$ は$0$ と $1$ のみを受理する。
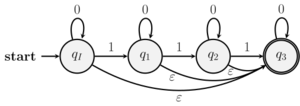
例 6 ($0$ と $1$ からなる有限記号列のうち、$1$ をちょうど3個含む記号列全体を受理する有限オートマトン)
\begin{align*} Q&=\mathsetextension{q_{I}, q_{1}, q_{2}, q_{3}} \\ \Sigma&=\mathsetextension{0, 1} \\ \Delta&=\mathsetextension{(q_{I}, 0, q_{I}), (q_{I}, 1, q_{1}), (q_{1}, 0, q_{1}), (q_{1}, 1, q_{2}), (q_{2}, 0, q_{2}), (q_{2}, 1, q_{3}), (q_{3}, 0, q_{3})} \\ F&=\mathsetextension{q_{3}} \end{align*} とすると、$\mathautomaton{A}=(Q, \Sigma, \Delta, q_{I}, F)$ は有限オートマトンである。
この有限オートマトン $\mathautomaton{A}$ は $0$ と $1$ からなる有限記号列のうち、$1$ をちょうど3個含む記号列のみを受理する。
例 7 ($0$ と $1$ からなる有限記号列のうち、$1$ を高々3個含む記号列全体を受理する有限オートマトン その1)
\begin{align*} Q&=\mathsetextension{q_{I}, q_{1}, q_{2}, q_{3}}\\ \Sigma&=\mathsetextension{0, 1}\\ \Delta&=\mathsetextension{(q_{I}, 0, q_{I}), (q_{I}, 1, q_{1}), (q_{1}, 0, q_{1}), (q_{1}, 1, q_{2}), (q_{2}, 0, q_{2}), (q_{2}, 1, q_{3}), (q_{3}, 0, q_{3}), (q_{I}, \emptyword, q_{3}), (q_{1}, \emptyword, q_{3}), (q_{2}, \emptyword, q_{3})}\\ F&= \mathsetextension{q_{3}}\end{align*} とすると、$\mathautomaton{A}=(Q, \Sigma, \Delta, q_{I}, F)$ は有限オートマトンである。
この有限オートマトン $\mathautomaton{A}$ は $0$ と $1$ からなる有限記号列のうち、$1$ を高々3個含む記号列のみを受理する。
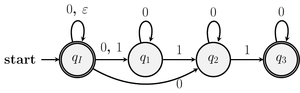
例 8 ($0$ と $1$ からなる有限記号列のうち、$1$ を高々3個含む記号列全体を受理する有限オートマトン その2)
\begin{align*} Q&=\mathsetextension{q_{I}, q_{1}, q_{2}, q_{3}}\\ \Sigma&=\mathsetextension{0, 1}\\ \Delta&=\mathsetextension{(q_{I}, \emptyword, q_{I}), (q_{I}, 0, q_{I}), (q_{I}, 0, q_{1}), (q_{I}, 0, q_{2}), (q_{I}, 0, q_{3}), (q_{I}, 1, q_{1}), (q_{1}, 0, q_{1}), (q_{1}, 1, q_{2}), (q_{2}, 0, q_{2}), (q_{2}, 1, q_{3})}\\ F&= \mathsetextension{q_{I},q_{3}}\end{align*} とすると、$\mathautomaton{A}=(Q, \Sigma, \Delta, q_{I}, F)$ は有限オートマトンである。
この有限オートマトン $\mathautomaton{A}$ も $0$ と $1$ からなる有限記号列のうち、$1$ を高々3個含む記号列のみを受理する。
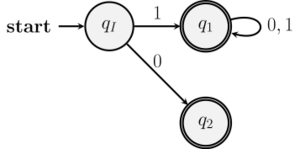
例 9 (自然数の二進表現全体を受理する有限オートマトン)
\begin{align*}Q&=\mathsetextension{q_{I}, q_{1}, q_{2}}\\ \Sigma&=\mathsetextension{0, 1}\\ \Delta&=\mathsetextension{(q_{I}, 0, q_{2}), (q_{I}, 1, q_{1}), (q_{1}, 0, q_{1}), (q_{1}, 1, q_{1})}\\ F&= \mathsetextension{q_{1}, q_{2}}\end{align*}
とすると、$\mathautomaton{A}=(Q, \Sigma, \Delta, q_{I}, F)$ は有限オートマトンである。
この有限オートマトン $\mathautomaton{A}$ は 自然数の二進表現のみを受理する。
正規言語、正規表現との関係
この節では有限オートマトン、正規言語および正規表現の関係を述べる。
定理 10
言語 $L$ について以下は同値である。
- $L$ は正規言語である。
- $L=\interpret{\alpha}$ なる正規表現 $\alpha$ が存在する。
- $L$ を受理する有限オートマトンが存在する。
この定理の証明は、項目正規言語を参照せよ。
反復補題(ポンピング補題)
この節では反復補題(pumping lemma)について述べる[1]。 反復補題はポンピング補題やポンプ補題と呼ばれることもある。
反復補題はある記号列の集合が正規言語ではない証明などに用いられる。
補題 11 (反復補題)
状態集合の大きさが $n$ の有限オートマトン $\mathautomaton{A}$ に記号列 $w$ が受理されるとする。
$\left|w\right|\gt n$ であるとき、次の四条件を満たす記号列 $x$, $y$, $z$ が存在する。
- $w=xyz$。
- $\left|y\right|\gt 0$。
- 任意の$m\in\mathnat$に対して、記号列 $xy^{m}z$ は$\mathautomaton{A}$ に受理される。
- $|xy|\leq n$。
Proof.
有限オートマトン $\mathautomaton{A}=(Q, \Sigma, \Delta, q_{I}, F)$ に $w$ が受理されるとする。 以下 $n:=\left|Q\right|$, $l:=\left|w\right|$, $l\gt n$ とする。
有限オートマトン $\mathautomaton{A}$ に $w$ が受理されることから、
- $w=a_{1}a_{2} \dots a_{k}$ (ただし、各 $i=1, \dots, k$ について $a_{i}\in \Sigma\cup\{\emptyword\}$)。
- すべての $i\in \{1, \dots, k\}$ について $(q_{i-1}, a_{i}, q_{i})\in \Delta$。
- $q_{0}=q_{I}$, $q_{k}\in F$。
を満たす状態の列 $q_{0}, q_{1}, \dots, q_{k}$ と記号の列 $a_{1}, a_{2}, \dots, a_{k}$が存在する (ただし、$k\geq l$)。
$l\gt n$ から長さが $n$ の $w$ の接頭語 $w_{0}$ が存在する。 すると、$q_{0}, q_{1}, \dots, q_{k}$ の部分列であって、$w_{0}$ による $\mathautomaton{A}$ の状態遷移 $$q_{0}, q_{1}, \dots, q_{k_{0}}$$ が存在する(ただし $n\leq k_{0}\leq k$)。
すると、鳩ノ巣原理より
- $(q_{i-1}, a_{i}, q_{i})$, $(q_{i+j-1}, a_{i+j}, q_{i+j})\in \Delta$
(ただし、$a_{i}\neq\emptyword$, $a_{i+j}\neq\emptyword$)
- $q_{i}=q_{i+j}$
という条件を満たす自然数の組 $(i, j)$ (ただし $0\leq i\leq k_{0}$, $0< j\leq k_{0}$)が少なくとも1つ存在する。 以下その $i$, $j$ を固定する。
\begin{align*} x&:=a_{1}a_{2}\ldots a_{i}, \\ y&:=a_{i+1}a_{i+2}\ldots a_{i+j}, \\ z&:=a_{i+j+1}a_{i+j+2}\ldots a_{k},\end{align*} とすると、$w=xyz$ である。また、$a_{i+j}\neq\emptyword$ であるから $\left|y\right|\gt 0$。 さらに、定義より $xy$ は $w_{0}$ の部分列であるから、$|xy|\leq n$。
任意の$m\in\mathnat$に対して、記号列 $xy^{m}z$ が $\mathautomaton{A}$ に受理されることを示す。
以下、記号列 $x$, $y$, $z$ による $\mathautomaton{A}$ の状態遷移をそれぞれ \begin{align*}Q_{x}&=q_{0}, \dots, q_{i}, \\ Q_{y}&=q_{i+1}, \dots, q_{i+j}, \\ Q_{z}&=q_{i+j+1}, \dots, q_{k}, \end{align*} と書くことにする。
$m=0$ のときを示す。
$q_{i}=q_{i+j}$ に注意すると、$(q_{i}, a_{i+j+1}, q_{i+j+1})\in \Delta$ である。 よって、 $$Q_{x}Q_{z}=q_{0}, \dots, q_{i}, q_{i+j+1}, \dots, q_{k}$$ は記号列 $xz$ による $\mathautomaton{A}$ の状態遷移である。 $q_{0}=q_{I}$, $q_{k}\in F$ であるから、$xz$($=xy^{0}z$) は $\mathautomaton{A}$ に受理される。
$m\gt 0$ のときを示す。
$q_{i}=q_{i+j}$ に注意すると、$(q_{i+j}, a_{i+j+1}, q_{i+1})\in \Delta$ である。 $$Q_{x}\overbrace{Q_{y}\dots Q_{y}}^{m\text{個}}Q_{z}=q_{0}, \dots, q_{i}, \overbrace{q_{i+1}, \dots, q_{i+j}, q_{i+1}, \dots, q_{i+j}}^{\text{$q_{i+1}, \dots, q_{i+j}$ の反復が $m$回}}, q_{i+j+1}, \dots, q_{k}$$ は記号列 $xy^{m}z$ による $\mathautomaton{A}$ の状態遷移である。 $q_{0}=q_{I}$, $q_{k}\in F$ であるから、$xy^{m}z$ は $\mathautomaton{A}$ に受理される。
□反復補題(ポンピング補題)の系
系 12
状態集合の大きさが $n$ の有限オートマトン $\mathautomaton{A}$ について、有限オートマトン $\mathautomaton{A}$ に受理される記号列が存在するとき、長さ $n$ 未満の記号列で有限オートマトン $\mathautomaton{A}$ に受理される記号列が存在する。
Proof.
状態集合の大きさが $n$ の有限オートマトン $\mathautomaton{A}$ について、記号列 $w$ が有限オートマトン $\mathautomaton{A}$ に受理されると仮定する。
$|w| \lt n$ のときは明らか。$|w| \geq n$ と仮定する。すると反復補題から,次の四条件を満たす記号列 $x$, $y$, $z$ が存在する。
- $w=xyz$。
- $\left|y\right|\gt 0$。
- 任意の$m\in\mathnat$に対して、記号列 $xy^{m}z$ は$\mathautomaton{A}$ に受理される。
- $|xy|\leq n$。
このとき、$xz$ は $\mathautomaton{A}$ に受理される。このとき、$|w| \gt |xz|$ に注意する。$|xz| \lt n$ ならば、$xz$ が求める記号列である。そうではないとき、$w = xz$ として、同様に $\mathautomaton{A}$ に受理される記号列で $|w|$ より長さの短いものが存在することが、反復補題によりわかる。この操作は $|w| \lt n$ となるまで、何度でも行うことができるから、長さ $n$ 未満の記号列で有限オートマトン $\mathautomaton{A}$ に受理される記号列が存在することがわかる。
□$\emptyword$ 動作なしの有限オートマトン
この項では $\emptyword$ 動作なしの有限オートマトン(finite automaton without $\emptyword$-transitions) について述べる。
定義 13 ($\emptyword$ 動作なしの有限オートマトン)
有限オートマトン $\mathautomaton{A}=(Q, \Sigma, \Delta, q_{I}, F)$ が 次の条件を満たすとき、 $\mathautomaton{A}$ は $\emptyword$ 動作なしの有限オートマトン(finite automaton without $\emptyword$-transitions)であると言う:
- $(q, a, q')\in \Delta$ に対して $a=\emptyword$ ならば $q=q'$
命題 14
任意の有限オートマトンに対して、それと等価な $\emptyword$ 動作なしの有限オートマトンが存在する。
Proof.
$\mathautomaton{A}=(Q, \Sigma, \Delta, q_{I}, F)$ を有限オートマトンとする。
$q\in Q$, $a\in \Sigma$ にたいして、集合 $\mathof{C}{q, a}$ を次のように定める: \[ \mathof{C}{q, a}=\mathsetintension{(q, a, q')}{ \text{記号列 $a$ による $q$ から $q'$ への $\mathautomaton{A}$ の状態遷移が存在する}}. \]
$\mathof{C_{\emptyword}}{q_{I}}$ を次のように定義する: \[\mathof{C_{\emptyword}}{q_{I}}=\mathsetintension{q'\in Q}{\text{記号列 } \emptyword \text{ による } q_{I} \text{ から } q' \text{ への } \mathautomaton{A} \text{ の状態遷移が存在する} }. \]
次のように集合 $\Delta'_{0}$, $\Delta'_{\emptyword}$ および $\Delta'$ を次のように定める: \begin{align*} \Delta'_{0}&=\bigcup_{q\in Q, a\in \Sigma} \mathof{C}{q, a}, \\ \Delta'_{\emptyword}&=\mathsetintension{(q, \emptyword, q)}{q\in Q}, \\ \Delta'&=\Delta'_{0}\cup \Delta'_{\emptyword}. \end{align*} また、 \[F'= \begin{cases} F, & \text{if } F\cap\mathof{C_{\emptyword}}{q_{I}}=\emptyset, \\ F \cup \mathsetextension{q_{I}}, & \text{if } F\cap\mathof{C_{\emptyword}}{q_{I}}\neq\emptyset. \end{cases} \] とする。 このとき$\mathautomaton{A}'=(Q, \Sigma, \Delta', q_{I}, F')$ は $\emptyword$ 動作なしの有限オートマトンである。
記号列 $w\neq\emptyword$ に対して、以下が同値であることを示す:
- 記号列 $w$ による $q$ から $q'$ への $\mathautomaton{A}$ の状態遷移が存在する
- 記号列 $w$ による $q$ から $q'$ への $\mathautomaton{A}'$ の状態遷移が存在する
次のように集合 $\Delta_{\emptyword}$ および $\Delta_{0}$ を次のように定める。 \begin{align*} \Delta_{\emptyword}&=\mathsetintension{(q, a, q')\in \Delta}{a=\emptyword\text{ かつ }q\neq q'}, \\ \Delta_{0}&=\Delta\setminus\Delta_{\emptyword}. \end{align*} 以下 $\Delta_{0} \subseteq \Delta'_{0}$ に注意する。
1 $\Rightarrow$ 2: 記号列 $w$ による $q$ から $q'$ への $\mathautomaton{A}$ の状態遷移が存在すると仮定する。 $\left|w\right|$ に対する帰納法により示す。
$\left|w\right|=1$ のとき: 記号列 $w$ による $q$ から $q'$ への $\mathautomaton{A}$ の状態遷移が存在することから $(q, w, q')\in \mathof{C}{q, w}$。 よって、$(q, w, q')\in \Delta'$。よって、$q$ から $q'$ への $\mathautomaton{A}'$ の状態遷移が存在する。
$\left|w\right|\gt 1$ のとき: $w=w_{0}a$ とおく(ただし、$a\in\Sigma$)。
記号列 $w$ による $q$ から $q'$ への $\mathautomaton{A}$ の状態遷移が存在することから
- $w=a_{1}a_{2} \dots a_{k}$ (ただし、各 $i=1, \dots, k$ について $a_{i}\in \Sigma\cup\{\emptyword\}$)。
- すべての $i\in \{1, \dots, k\}$ について $(q_{i-1}, a_{i}, q_{i})\in \Delta$。
- $q_{0}=q$, $q_{k}=q'$。
を満たす状態の列 $q_{0}, q_{1}, \dots, q_{k}$ と記号の列 $a_{1}, a_{2}, \dots, a_{k}$が存在する (ただし、$k\geq l$)。 このとき、$w_{0}=a_{1}\dots a_{k_{0}}$, $a=a_{k_{0}+1}$, $1\leq k_{0}\lt k$ を満たす $k_{0}$ が存在する。
すると、$q=q_{0}, q_{1}, \dots, q_{k_{0}}$ は記号列 $w_{0}$ による $q$ から $q_{k_{0}}$ への $\mathautomaton{A}$ の状態遷移である。 また、$q_{k_{0}}, q_{k_{0}+1}, \dots, q_{k}=q'$ は記号列 $a$ による $q_{k_{0}}$ から $q'$ への $\mathautomaton{A}$ の状態遷移である。
帰納法の仮定から 記号列 $w_{0}$ による $q$ から $q_{k_{0}}$ への $\mathautomaton{A}'$ の状態遷移が存在する。 また、記号列 $a$ による $q_{k_{0}}$ から $q'$ への $\mathautomaton{A}$ の状態遷移が存在することから $(q_{k_{0}}, a, q')\in \mathof{C}{q_{k_{0}}, a}$。ゆえに、記号列 $w=w_{0}a$ による $q$ から $q'$ への $\mathautomaton{A}'$ の状態遷移が存在する。
2 $\Rightarrow$ 1: 記号列 $w$ による $q$ から $q'$ への $\mathautomaton{A}'$ の状態遷移が存在すると仮定する。 $\left|w\right|$ に対する帰納法により示す。
$\left|w\right|=1$ のとき: 記号列 $w$ による $q$ から $q'$ への $\mathautomaton{A}'$ の状態遷移が存在することから
- $w=a_{1}a_{2} \dots a_{k}$ (ただし、各 $i=1, \dots, k$ について $a_{i}\in \Sigma\cup\{\emptyword\}$)。
- すべての $i\in \{1, \dots, k\}$ について $(q_{i-1}, a_{i}, q_{i})\in \Delta'$。
- $q_{0}=q$, $q_{k}=q'$。
を満たす状態の列 $q_{0}, q_{1}, \dots, q_{k}$ と記号の列 $a_{1}, a_{2}, \dots, a_{k}$が存在する (ただし、$k\geq l$)。 $\left|w\right|=1$ であるから、 \[a_{i}= \begin{cases} w & i=k_{0} \\ \emptyword & i\neq k_{0} \end{cases} \] を満たす $1\leq k_{0}$ が存在する。このとき、$\Delta'$ の定義から \[q_{i}= \begin{cases} q & i\lt k_{0} \\ q' & k_{0}\leq i \end{cases} \] であって、$(q, w, q')\in \Delta'_{0}$ である。 $\Delta'_{0}$ の定義から $(q, w, q')\in \mathof{C}{q, w}$。 これは記号列 $w$ による $q$ から $q'$ への $\mathautomaton{A}$ の状態遷移が存在することを意味する。
$\left|w\right|\gt 1$ のとき: $w=w_{0}a$ とおく(ただし、$a\in\Sigma$)。
記号列 $w$ による $q$ から $q'$ への $\mathautomaton{A}'$ の状態遷移が存在することから
- $w=a_{1}a_{2} \dots a_{k}$ (ただし、各 $i=1, \dots, k$ について $a_{i}\in \Sigma\cup\{\emptyword\}$)。
- すべての $i\in \{1, \dots, k\}$ について $(q_{i-1}, a_{i}, q_{i})\in \Delta$。
- $q_{0}=q$, $q_{k}=q'$。
を満たす状態の列 $q_{0}, q_{1}, \dots, q_{k}$ と記号の列 $a_{1}, a_{2}, \dots, a_{k}$が存在する (ただし、$k\geq l$)。 このとき、$w_{0}=a_{1}\dots a_{k_{0}}$, $a=a_{k_{0}+1}$, $1\leq k_{0}\lt k$ を満たす $k_{0}$ が存在する。
すると、$q=q_{0}, q_{1}, \dots, q_{k_{0}}$ は記号列 $w_{0}$ による $q$ から $q_{k_{0}}$ への $\mathautomaton{A}'$ の状態遷移である。 また、$q_{k_{0}}, q_{k_{0}+1}, \dots, q_{k}=q'$ は記号列 $a$ による $q_{k_{0}}$ から $q'$ への $\mathautomaton{A}'$ の状態遷移である。
帰納法の仮定から 記号列 $w_{0}$ による $q$ から $q_{k_{0}}$ への $\mathautomaton{A}$ の状態遷移が存在し、 また、記号列 $a$ による $q_{k_{0}}$ から $q'$ への $\mathautomaton{A}$ の状態遷移が存在する。ゆえに、記号列 $w=w_{0}a$ による $q$ から $q'$ への $\mathautomaton{A}$ の状態遷移が存在する。
以上を踏まえて、$L(\mathautomaton{A})=L(\mathautomaton{A}')$ を示す。
$w\in L(\mathautomaton{A})$ を仮定する。 $w=\emptyword$ のとき、$F\cap\mathof{C_{\emptyword}}{q_{I}}\neq\emptyset$ である。 ゆえに、$q_{I}\in F'$。$(q_{I}, \emptyword, q_{I})\in \Delta'$ に注意すると、 $\emptyword$ による $q_{I}$ から $q_{I}$ への $\mathautomaton{A}'$ の状態遷移が存在するので、 $\emptyword\in L(\mathautomaton{A}')$。
$w\neq \emptyword$ のとき、 記号列 $w$ による $q_{I}$ から $q\in F$ への $\mathautomaton{A}$ の状態遷移が存在することから、 記号列 $w$ による $q_{I}$ から $q\in F'$ への $\mathautomaton{A}'$ の状態遷移が存在することが速やかにわかる。ゆえに $w\in L(\mathautomaton{A}')$。
以上より $L(\mathautomaton{A})\subseteq L(\mathautomaton{A}')$。
$w\in L(\mathautomaton{A}')$ を仮定する。 $w=\emptyword$ のとき、$(q_{I}, \emptyword, q_{I})\in \Delta'$ かつ $q_{I}\in F'$ である。
$F\cap\mathof{C_{\emptyword}}{q_{I}}=\emptyset$ のとき、$q_{I}\notin F$。また、$F=F'$ である。 まとめて、$q_{I}\notin F=F'\ni q_{I}$。これは矛盾である。 よって、$F\cap\mathof{C_{\emptyword}}{q_{I}}\neq\emptyset$ である。 ゆえに、$q\in \mathof{C_{\emptyword}}{q_{I}}$, $q\in F$ を満たす状態 $q\in Q$ が存在する。 $q\in \mathof{C_{\emptyword}}{q_{I}}$ であるから、 $\emptyword$ による $q_{I}$ から $q$ への $\mathautomaton{A}$ の状態遷移が存在する。 $q\in F$ であるから $\emptyword\in L(\mathautomaton{A}')$。
$w\neq \emptyword$ のとき、 記号列 $w$ による $q_{I}$ から $q\in F$ への $\mathautomaton{A}'$ の状態遷移が存在することから、 記号列 $w$ による $q_{I}$ から $q\in F'$ への $\mathautomaton{A}$ の状態遷移が存在することが速やかにわかる。
以上より $L(\mathautomaton{A}')\subseteq L(\mathautomaton{A})$。
$L(\mathautomaton{A})\subseteq L(\mathautomaton{A}')$ より$L(\mathautomaton{A})=L(\mathautomaton{A}')$。 $\mathautomaton{A}'$ が $\emptyword$ 動作なしの有限オートマトンであるから、命題の主張を得る。
□決定性有限オートマトン
この項では決定性有限オートマトン(deterministic finite automaton)について述べる。
定義 15 (決定性有限オートマトン)
$\emptyword$ 動作なしの有限オートマトン $\mathautomaton{A}=(Q, \Sigma, \Delta, q_{I}, F)$ が次の条件を満たすとき、$\mathautomaton{A}$ は決定性有限オートマトン(deterministic finite automaton)であると言う:
- 各 $(q, a) \in Q\times \Sigma$ という組に対して、$(q, a, q')\in \Delta$ という形の元は高々一個
有限オートマトン $\mathautomaton{A}$ が決定性有限オートマトンとは限らないことを明示したいときに、 $\mathautomaton{A}$ は非決定性有限オートマトン(nondeterministic finite automaton)であると言うことがある。
命題 16
任意の有限オートマトンに対して、それと等価な決定性有限オートマトンが存在する。
Proof.
$\mathautomaton{A}_{0}=(Q_{0}, \Sigma, \Delta_{0}, q_{I}, F_{0})$ を有限オートマトンとする。 命題 16 から $\mathautomaton{A}_{0}$ と等価な $\emptyword$ 動作なしの有限オートマトン $\mathautomaton{A}=(Q, \Sigma, \Delta, q_{I}, F)$ が存在する。
$S\subseteq Q$, $a\in (\Sigma \cup \mathsetextension{\emptyword})$ に対して、集合 $\mathof{T}{S, a}$ を次のように定める: \[ \mathof{T}{S, a}=\mathsetintension{q'\in Q}{(q, a, q')\in\Delta \text{ for } q\in S}. \] 次のように集合 $\Delta'$, $F'$ を定める。 \begin{align*} \Delta' &=\mathsetintension{(S, a, \mathof{T}{S, a})}{S\subseteq Q, a\in (\Sigma \cup \mathsetextension{\emptyword}) } \\ F' &=\mathsetintension{S\subseteq Q}{S\cap F\neq \emptyset} \end{align*}
このとき、$\mathautomaton{A}'=(\mathpowerset{Q}, \Sigma, \Delta', \mathsetextension{q_{I}}, F')$ は決定性有限オートマトンである。
$\mathof{L}{\mathautomaton{A}}=\mathof{L}{\mathautomaton{A}'}$ を示す。
まず、$\mathof{L}{\mathautomaton{A}}\subseteq\mathof{L}{\mathautomaton{A}'}$ を示すために次の命題($*$)を示す:
($*$) 記号列 $w$ による $q_{I}$ から $q$ への $\mathautomaton{A}$ の状態遷移が存在するとき、次を満たす $S\in \mathpowerset{Q}$ が存在する:
- $q\in S$。
- 記号列 $w$ による $\mathsetextension{q_{I}}$ から $S$ への $\mathautomaton{A}'$ の状態遷移が存在する。
記号列 $w$ による $q_{I}$ から $q$ への $\mathautomaton{A}$ の状態遷移 $(q_{I}=)q_{0}, \dots, q_{n}(=q)$ が存在すると仮定する。 ($*$) の 1., 2. を満たす $S$ が存在することを $n$ についての帰納法により示す。
$n=0$ のときは明らか。
$n\gt 0$ のとき、次を満たす $w'\in \kleenecl{\Sigma}$, $a\in \Sigma$ が存在する:
- $w=w'a$。
- $(q_{n-1}, a, q_{n})\in \Delta$。
帰納法の仮定から、$q_{n-1}\in S'$、 記号列 $w'$ による $\mathsetextension{q_{I}}$ から $S'$ への $\mathautomaton{A}'$ の状態遷移が存在する。 $(q_{n-1}, a, q_{n})\in \Delta$ より、次を満たす $S\in \mathpowerset{Q}$ が存在する:
- $q_{n}\in S$。
- $(S', a, S)\in \Delta'$。
ゆえに、$q\in S$ で 記号列 $w$ による $\mathsetextension{q_{I}}$ から $S$ への $\mathautomaton{A}'$ の状態遷移が存在する。 以上より ($*$) は示された。
さて、$w\in \mathof{L}{\mathautomaton{A}}$ を仮定する。 すると、記号列 $w$ による $q_{I}$ から $q\in F$ への $\mathautomaton{A}$ の状態遷移が存在する。 (*) より次を満たす $S\in \mathpowerset{Q}$ が存在する:
- $q\in S$。
- 記号列 $w$ による $\mathsetextension{q_{I}}$ から $S$ への $\mathautomaton{A}'$ の状態遷移が存在する。
$q\in S$ より $S\cap F\neq \emptyset$ であるから、$S\in F'$。 ゆえに、$w\in \mathof{L}{\mathautomaton{A}'}$。 よって、$\mathof{L}{\mathautomaton{A}}\subseteq \mathof{L}{\mathautomaton{A}'}$。
次に $\mathof{L}{\mathautomaton{A}'}\subseteq\mathof{L}{\mathautomaton{A}}$ を示すために次の命題($**$)を示す:
($**$) 記号列 $w$ による $\mathsetextension{q_{I}}$ から $S$ への $\mathautomaton{A}'$ の状態遷移が存在するとき、 任意の $q\in S$ に対して記号列 $w$ による $q_{I}$ から $q$ への $\mathautomaton{A}$ の状態遷移が存在する。
記号列 $w$ による $\mathsetextension{q_{I}}$ から $S$ への $\mathautomaton{A}$ の状態遷移 $(\mathsetextension{q_{I}}=)S_{0}, \dots, S_{n}(=S)$ が存在すると仮定する。 任意の $q\in S$ に対して記号列 $w$ による $q_{I}$ から $q$ への $\mathautomaton{A}$ の状態遷移が存在することを $n$ についての帰納法により示す。
$n=0$ のときは明らか。
$n\gt 0$ のとき、$q\in S$ とする。 このとき、次を満たす $w'\in \kleenecl{\Sigma}$, $a\in \Sigma$ が存在する:
- $w=w'a$。
- $(S_{n-1}, a, S)\in \Delta'$。
$(S_{n-1}, a, S)\in \Delta'$ のであるから、$(q', a, q)\in \Delta$ を満たす $q'\in S_{n-1}$ が存在する。 帰納法の仮定から記号列 $w'$ による $q_{I}$ から $q'$ への $\mathautomaton{A}$ の状態遷移が存在する。 $(q', a, q)\in \Delta$ から、 帰納法の仮定から記号列 $w$ による $q_{I}$ から $q$ への $\mathautomaton{A}$ の状態遷移が存在する。 以上より ($**$) は示された。
さて、$w\in \mathof{L}{\mathautomaton{A}'}$ を仮定する。 すると、記号列 $w$ による $\mathsetextension{q_{I}}$ から $S\in F'$ への $\mathautomaton{A}'$ の状態遷移が存在する。 このとき、$S\cap F\neq \emptyset$ であるから、$q\in S$ かつ $q\in F$ を満たす $q$ が存在する。 ($**$) から記号列 $w$ による $q_{I}$ から $q$ への $\mathautomaton{A}$ の状態遷移が存在する。 $q\in F$ であるから、$w\in \mathof{L}{\mathautomaton{A}}$。 よって、$\mathof{L}{\mathautomaton{A}'}\subseteq\mathof{L}{\mathautomaton{A}}$。
以上より $L(\mathautomaton{A})=L(\mathautomaton{A}')$。 $\mathautomaton{A}'$ が決定性有限オートマトンであるから、命題の主張を得る。
□参考文献
- 新屋 良磨、オートマトン理論再考、コンピュータ ソフトウェア、2017、34 巻、3 号、p. 3_3-3_35、公開日 2017/09/25、Print ISSN 0289-6540、[1]、[2]
- 五十嵐喜英他、『数理情報科学シリーズ 24 オートマトンと形式言語の基礎』、牧野書店、2011
- Martin Aigner,Guenter M. Ziegler,Karl H. Hofmann, "Proofs from THE BOOK", Springer, 2004
脚注
- ↑ Martin Aigner,Guenter M. Ziegler,Karl H. Hofmann, ["Proofs from THE BOOK"], Springer, 2004 によると、一般に定理が補題と呼ばれる条件は「広範囲の応用例を持つ」「一見して完璧に明らか」「証明も含めて美しい」の三条件を満たすことである。
関連項目
| 文法のタイプ | 言語のクラス | 計算モデル |
|---|---|---|
| タイプ0 | 句構造言語 | Turingマシン |
| タイプ1 | 文脈依存言語 | 線形有界オートマトン |
| タイプ2 | 文脈自由言語 | プッシュダウン・オートマトン |
| タイプ3 | 正規言語 | 有限オートマトン |