曲線の変分論

この記事では擬Riemann多様体上の曲線の変分論について解説する。 曲線の変分論において主に考察の対象となるのは測地線の“束”である。 測地線の束を考察することで種々の大域的な結果につながる。 非退化な不定値計量を持つ多様体、すなわち擬Riemann多様体(pseudo-Riemannian manifold)上で統一的述べれる部分まで曲線の変分論を展開し、その後Riemann多様体、Lorentz多様体に特化した議論を行い、いくつかの大域的性質を導く。

擬Riemann多様体上の曲線の変分論

曲線の変分

曲線を“平たく”並べると曲面が作られる。 この小さな曲面が曲線の変分論で主に考察される基本的な対象である。

定義 1 (曲線の変分)

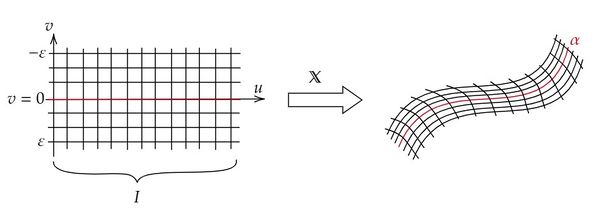
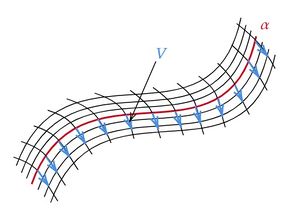
滑らかな曲線 $\alpha:I\ni u\mapsto \alpha(u)\in M$ の変分 (variation) とは、滑らかな写像 $\mathbb{X}:I\times(-\epsilon,\epsilon)\ni (u,v)\mapsto \mathbb{X}(u,v)\in M$ で、$\mathbb{X}(u,0)=\alpha(u)$ となるものを言う。 与えられた $v$ に対して曲線 $u\mapsto\mathbb{X}(u,v)$ で定義される曲線を縦方向曲線 (longitudial curve)、与えられた $u$ に対して曲線 $v\mapsto\mathbb{X}(u,v)$ で定義される曲線を横断的曲線 (transversal curve)と呼ぶ。 また、曲線 $\alpha(u)$ に沿うベクトル場 $V(u):=\frac{\partial}{\partial v}\mathbb{X}(u,0)$ を変分 $\mathbb{X}$ の変分ベクトル場 (variation vector field)と呼ぶ。 この記事を通して曲線 $\alpha$ の接ベクトル場を $\dot{\alpha}(u):=\frac{d\alpha}{du}$ と書くことにする。

チャートに関して変分が $\mathbb{X}(u,v)=(x^1(u,v),\cdots,x^n(u,v))$ で与えられるとき、$V(u)=\sum_i\frac{\partial x^i(u,0)}{\partial v}\partial_i$ は $\alpha(u)$ 上で定義されるベクトル場を定める。これはチャートの取り方に寄らない。

変分ベクトル場は曲線 $\alpha$ を基準にしたときの"隣の"曲線の相対位置を示す位置ベクトルを無限小化したものである。

以下では区分的に滑らかな曲線について考える。 単に滑らかとせず、区分的滑らかとする理由としては今後種々の所望の条件を満たす曲線を構成する場合、しばしば１つまたは２つの折点を持つ滑らかな曲線を利用することがあるからである。

定義 2 (区分的滑らかな曲線)

多様体 $M$ 上の区分的滑らかな曲線 $\alpha:(a,b)\rightarrow M$ とは、有限個の $u_i,\ (0\le i\le n)$ で $a=u_0<u_1<\cdots<u_{n-1}<u_n=b$ を満たすものがあり、$\alpha|_{(u_{i-1},u_i)}:(u_{i-1},u_i)\rightarrow M$ が滑らかで、かつ $$ \begin{align} \dot{\alpha}(u_{i-1}+0)&:=\lim_{u\rightarrow u_{i-1}+0}\frac{d\alpha}{du}\in T_{\alpha(u_{i-1})}M,\\ \dot{\alpha}(u_i-0)&:=\lim_{u\rightarrow u_i-0}\frac{d\alpha}{du}\in T_{\alpha(u_i)}M \end{align} $$ が定まる曲線のことである。また $$ \begin{align} \Delta\alpha(u_i):=\dot{\alpha}(u_i+0)-\dot{\alpha}(u_i-0) \end{align} $$ と定めるとき、$\Delta\alpha(u_i)\ne0$ となる $i\in\{1,\cdots,n\}$ は高々有限個しかないものとする。 $u_i$ 達を折点(break)と呼ぶ。 曲線 $\alpha$ の定義域は、$[a,b],[a,b),(a,b]$ などでもよい。

折点を $u=u_i,\ (1\le i\le r)$ とする区分的滑らかな曲線 $u\mapsto\alpha(u)$ に対しても変分 $\mathbb{X}(u,v)$ を同様に定義する。 ただし、全ての縦方向曲線 $u\mapsto\mathbb{X}(u,v)$ は区分的滑らかであるとし、その折点は $u=u_i\ (1\le i\le r)$ で与えられるとする。

曲線 $\alpha$ に対してその長さ $L(\alpha)$ が定義されるが、これは曲線の汎関数である。 曲線の変分を考えることで長さ汎関数の変分を考えることができる。 長さ汎関数の分析は曲線論において非常に重要である。 なぜなら、長さ汎関数の停留点として測地線が特徴づけられ、またその長さの極小性、極大性は長さ汎関数の2階変分を調べることで判明するからである。 さらに2階変分が不定値である場合は測地線はもはや長さに関して極小、極大とならず、従って大域的性質が判明する。

定義 3

$(M,g)$ を擬リーマン多様体とし、$\alpha:[a,b]\rightarrow M$ を区分的滑らかな曲線とする。 このとき、$\alpha$ の長さを $$ \begin{align} L(\alpha):=\int_a^b\left|\left|\dot{\alpha}(u)\right|\right|du \end{align} $$ と定義する。 ただし、$g(\dot{\alpha},\dot{\alpha})$ の符号を $\epsilon$ とするとき、$||\dot{\alpha}||:=\sqrt{\epsilon g(\dot{\alpha},\dot{\alpha})}$ と定義する。 また $\alpha(u)$ の任意の変分を $\mathbb{X}(u,v)$ とするとき、 $$ \begin{align} L(v):=\int_a^b\left|\left|\frac{\partial\mathbb{X}(u,v)}{\partial u}(u)\right|\right|du \end{align} $$ と書くことにする。 $\epsilon$ を $\alpha$ の符号と呼ぶことにする。

$\mathbb{X}(u,v)$ の縦方向曲線の接ベクトル場を $U(u,v):=\partial_u\mathbb{X}(u,v)$ とし、変分ベクトル場も $\mathbb{X}(u,v)$ 上に拡張し $V(u,v)=\partial_v\mathbb{X}(u,v)$ とする。 このとき、$U,V$ をさらに $M$ の近傍に任意に拡張し、$M$ の意味で共変微分したものを $\mathbb{X}(u,v)$ 上で考える（これは拡張の取り方に寄らない）。 すなわち $$ \begin{align} \nabla_UV(u,v):=\nabla_VU(u,v)=\sum_i\left(\frac{\partial^2x^i(u,v)}{\partial u\partial v}+\Gamma^i_{jk}U^jV^k\right)\partial_i \end{align} $$ とする。 特に、$\nabla_UV(u,0)=\nabla_VU(u,0)=\nabla_{\dot{\alpha}}V(u)=\nabla_V\dot{\alpha}(u)$ などと書くことにする。 また $\dot{\alpha}$ による共変微分はドットで表すことにする（$\nabla_{\dot{\alpha}}V=\dot{V}$ など）。

第一変分

定義 4 (長さ関数の第一変分)

$\alpha:[a,b]\rightarrow M$ を区分的滑らかな曲線とし、その任意の変分を $\mathbb{X}(u,v)$ とする。 このとき、$\mathbb{X}(u,v)$ に関する長さ関数の第一変分を $\frac{d L}{d v}(0)$ と定義する。

これを計算すると、 $$ \begin{align} \frac{\partial L}{\partial v}(0)&=\int^b_a\left(\frac{d}{dv}\sqrt{\epsilon g(U,U)}\right)_{v=0}du =\epsilon\int^a_b\left(\frac{g(\nabla_VU,U)}{||U||}\right)_{v=0}du\\ &=\epsilon\int^a_bg\left(\dot{V},\frac{\dot{\alpha}}{||\dot{\alpha}||}\right)du \end{align} $$